NH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DV
2
NP
0
19 tháng 6 2015
a, Gọi AC giao BD tai O
TAm giác OAB có
OA + OB > AB (1)
Tam giác OCD có
OC + OD > CD (2)
cộng vế với vế của (1) và (2) -=> AC + BD > AB + CD
GH
Gia Hân
VIP
18 tháng 7 2023
Bài 1:
a) Sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác OAB, OBC,OCD và ODA.
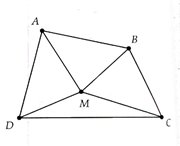
b) Chứng minh tổng hai đường chéo lớn hơn nửa chu vi tứ giác sử dụng kết quả của a).
Chứng minh tổng hai đường chéo nhỏ hơn chu vi tứ giác sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác ABC, ADC, ABD và CBD
Bài 3:
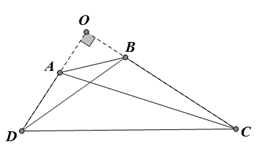
Gọi O là giao điểm AD và BC.
Ta có ˆC+⌢D=900�^+�⏜=900 nên ˆO=900�^=900
Áp dụng định lí Py – ta – go,
Ta có
AC2=OA2+OC2.��2=��2+��2.
BD2=OB2+OD2��2=��2+��2
Nên AC2+BD2=(OA2+OB2)+(OC2+OD2)=AB2+CD2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 7 2023
Bài 1: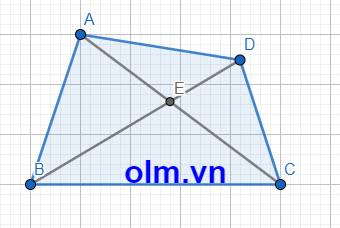 
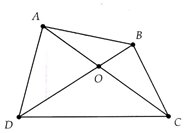
Gọi E là giao điểm của hai đường chéo AC và BD
Xét tam giác AEB ta có: AE + BE > AB (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Xét tam giác DEC ta có: DE + CE > DC (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Cộng vế với vế ta có: AE + BE + DE + CE > AB + DC
(AE + CE) + (BE + DE) > AB + DC
AC + BD > AB + DC
Tương tự ta có AC + BD > AD + BC
Kết luận: Trong một tứ giác tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối.
Nửa chu vi của tứ giác ABCD là: \(\dfrac{AB+BC+CD+DA}{2}\)
Theo chứng minh trên ta có:
\(\dfrac{AB+BC+CD+DA}{2}\)< \(\dfrac{\left(AB+CD\right)\times2}{2}\) = AB + CD (1)
Vì trong một tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại nên ta có:
AB + AD > BD
AB + BC > AC
BC + CD > BD
CD + AD > AC
Cộng vế với vế ta có:
(AB + BC + CD + DA)\(\times\)2 > (BD + AC ) \(\times\) 2
⇒AB + BC + CD + DA > BD + AC (2)
Kết hợp (1) và (2) ta có:
Tổng hai đường chéo của tứ giác lớn hơn nửa chu vi của tứ giác nhưng nhỏ hơn chu vi của tứ giác
B1
9 tháng 8 2017
a) tgiác ABC có MN là đường trung bình => MN // AC và MN = AC/2
tgiác DAC có PQ là đường trung bình => PQ // AC và PQ = AC/2
vậy: MN // PQ và MN = PQ => MNPQ là hình bình hành
mặt khác xét tương tự cho hai tgiác ABD và CBD ta cũng có:
NP // BD và NP = BD/2
do giả thiết AC_|_BD => AC_|_NP mà MN // AC => MN_|_NP
tóm lại MNPQ là hình chữ nhật (hbh có một góc vuông)
b) MNPQ là hình vuông <=> MN = NP <=> AC/2 = BD/2 <=> AC = BD
vậy điều kiện là: tứ giác ABCD có hai đường chéo vuông góc và bằng nhau
-------------
Nguồn:__|nobita|__
cách 2
a) Gọi QM giao AC tại F,AC giao BD tại K
ta có QM là đường trung bình của tam giác ADB
suy ra: QM// DB
ta có MN là đường trung bình của tam giác ABC
suy ra: MN// AC
ta có PN là đường trung bình của tam giác BCD
suy ra: PN// DB
ta có PQ là đường trung bình của tam giác ADC
suy ra: PQ// AC
từ đó ta có : QM//PN(cùng song song DB)
MN//PQ(cùng song song AC)
suy ra MNPQ là hình bình hành
QM//DB suy ra:góc AKB=góc AFM=90 độ
MN//AC suy ra:góc AFM= góc FMN= 90 độ
hình bình hành MNPQ có góc FMN=90 độ
suy ra MNPQ là hình chữ nhật
b)thuận:giả sử
MNPQ là hình vuông
suy ra MN=QM
ta có MN là đường trung bình của tam giác ABC
suy ra MN=1/2*AC
ta có QM là đường trung bình của tam giác ADC
suy ra QM=1/2*BD
MN=QM
suy ra BD= AC
vậy tứ giác ABCD cần thêm điều kiện là AC=BD để MNPQ là hình vuông
Bạn chứng minh đi