Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đề bài ko đúng bạn
Hàm \(f\left(x\right)=x^{2020}+2020x+1\) là hàm đa thức nên liên tục trên R
\(f\left(-2\right)=2^{2020}+1-4040>0\)
\(f\left(-1\right)=-2018< 0\)
\(\Rightarrow f\left(-2\right).f\left(-1\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;-1\right)\)
\(f\left(0\right)=1>0\)
\(\Rightarrow f\left(-1\right).f\left(0\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\)
Vậy pt đã cho có ít nhất 2 nghiệm (chính xác là có đúng 2 nghiệm)
Giải thích các bước giải:
sin 2x=cos xsin 2x=cos x
⇔sin 2x=sin (π2−x)⇔sin 2x=sin (π2-x)
⇔⇔ ⎡⎢⎣2x=π2−x+k2π (k∈Z)2x=π−π2+x+k2π (k∈Z)[2x=π2−x+k2π (k∈Z)2x=π−π2+x+k2π (k∈Z)
⇔⇔ ⎡⎢⎣3x=π2+k2π (k∈Z)x=π2+k2π (k∈Z)[3x=π2+k2π (k∈Z)x=π2+k2π (k∈Z)
⇔⇔ ⎡⎢ ⎢⎣x=π6+k2π3 (k∈Z)x=π2+k2π (k∈Z)[x=π6+k2π3 (k∈Z)x=π2+k2π (k∈Z)
Vậy S={π6+k2π3 (k∈Z),π2+k2π (k∈Z)
\(sinx=m^2-5m+1\Leftrightarrow sinx=\left(m-1\right)^2\) (1)
Pt có nghiệm: \(\Rightarrow-1\le sinx\le1\)
\(\Rightarrow\) \(0\le\left(m-1\right)^2\le1\)
\(\Rightarrow\)\(0\le m-1\le1\Rightarrow-1\le m\le0\)
Với \(m\in\left[-1;0\right]\) thì (1) có nghiệm.
Để pt (1) không có nghiệm \(\Rightarrow m\in\left(-\infty;-1\right)\cup\left(0;+\infty\right)\)
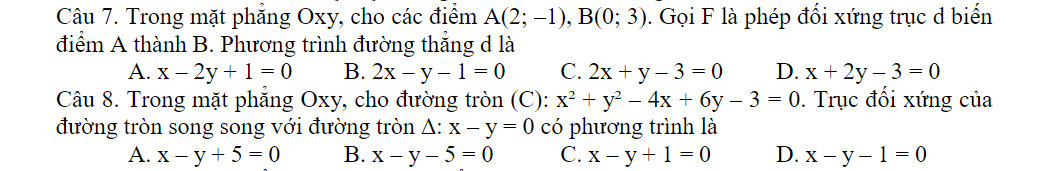Làm giúp mình 2 bài này với, có giải chi tiết. Mình cảm ơn nhiều
\(sin^2x+\sqrt{3}sinxcosx=1\)
\(\Leftrightarrow sin^2x+\sqrt{3}sinxcosx=sin^2x+cos^2x\)
\(\Leftrightarrow cosx\left(\sqrt{3}sinx-cosx\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}cosx=0\\\sqrt{3}sinx=cosx\end{cases}}\Leftrightarrow\orbr{\begin{cases}cosx=0\\tanx=\frac{1}{\sqrt{3}}\end{cases}}\)
Từ đây suy ra nghiệm.
Các chữ số được đặt trong các ô trống.
| . | . | . | . |
TH1: Số cần lập có chữ số 0:
Đưa 0 vào 3 cách
Đưa 1 vào 3 cách
Đưa 3 vào 2 cách
Lấy 1 số bất kì ô còn lại : 7 cách
=> TH1 có 126 số
TH2: Số cần lập không có chữ số 0:
Đưa 1 vào 4 cách
Đưa 3 vào 3 cách
Lấy 2 số bất kì đưa vào 2 ô còn lại : \(A^2_7\) cách
=> TH2 có 504 số
Vậy lập được tất cả 504 + 126 = 630 số
3.
\(4sinx+cosx+2cos\left(x+\dfrac{\pi}{3}\right)=2\)
\(\Leftrightarrow4sinx+cosx+cosx-\sqrt{3}sinx=2\)
\(\Leftrightarrow\left(4-\sqrt{3}\right)sinx+2cosx=2\)
\(\Leftrightarrow\sqrt{23-4\sqrt{3}}\left(\dfrac{4-\sqrt{3}}{\sqrt{23-4\sqrt{3}}}sinx+\dfrac{2}{\sqrt{23-4\sqrt{3}}}cosx\right)=2\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}\right)=\dfrac{2}{\sqrt{23-4\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}=\pm arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
4.
\(sinx+2cos\left(x+\dfrac{\pi}{3}\right)+4sin\left(x+\dfrac{\pi}{6}\right)+cosx=4\)
\(\Leftrightarrow sinx+cosx-\sqrt{3}sinx+2\sqrt{3}sinx+2cosx+cosx=4\)
\(\Leftrightarrow\left(1+\sqrt{3}\right)sinx+4cosx=4\)
\(\Leftrightarrow\sqrt{20+2\sqrt{3}}\left(\dfrac{1+\sqrt{3}}{\sqrt{20+2\sqrt{3}}}sinx+\dfrac{4}{\sqrt{20+2\sqrt{3}}}cosx\right)=4\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}\right)=\dfrac{4}{\sqrt{20+2\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}=\pm arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
b.
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}cos2x-\dfrac{1}{2}sin2x=-cosx\)
\(\Leftrightarrow cos\left(2x+\dfrac{\pi}{6}\right)=cos\left(x+\pi\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{6}=x+\pi+k2\pi\\2x+\dfrac{\pi}{6}=-x-\pi+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{6}+k2\pi\\x=-\dfrac{7\pi}{18}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
c.
\(\Leftrightarrow2cos4x.sin3x=2sin4x.cos4x\)
\(\Leftrightarrow cos4x\left(sin4x-sin3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\sin4x=sin3x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{\pi}{2}+k\pi\\4x=3x+k2\pi\\4x=\pi-3x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\\x=k2\pi\\x=\dfrac{\pi}{7}+\dfrac{k2\pi}{7}\end{matrix}\right.\)
2.
\(f\left(x\right)=\dfrac{1}{2}-\dfrac{1}{2}cos2x-\dfrac{\sqrt{3}}{2}sin2x-5\)
\(=-\dfrac{9}{2}-\left(\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x\right)\)
\(=-\dfrac{9}{2}-cos\left(2x-\dfrac{\pi}{3}\right)\)
Do \(-1\le-cos\left(2x-\dfrac{\pi}{3}\right)\le1\Rightarrow-\dfrac{11}{2}\le y\le-\dfrac{7}{2}\)
\(y_{min}=-\dfrac{11}{2}\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=1\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\)
\(y_{max}=-\dfrac{7}{2}\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=-1\Rightarrow x=\dfrac{2\pi}{3}+k\pi\)