K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
9 tháng 11 2019
Cách 1: Sử dụng các phép biến đổi tương đương để chứng minh bất đẳng thức.
Ta có:
Do đó: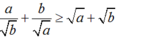 
(đpcm)
Cách 2: Sử dụng bất đẳng thức Cô-si để chứng minh bất đẳng thức.
Áp dụng bất đẳng thức Cô-si cho hai số dương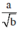 
và √b ta có:
Dấu “=” xảy ra khi và chỉ khi a= b > 0
NT
1
20 tháng 3 2018
a)\(a^2+ab+b^2=a^2+\dfrac{2ab}{2}+\left(\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}\)
\(=\left(a+\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}\ge0\forall a,b\)
b)\(a^4+b^4\ge a^3b+ab^3\)
\(\Leftrightarrow a^3\left(a-b\right)-b^3\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a^3-b^3\right)\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\left(a^2+ab+b^2\right)\ge0\forall a,b\)
PT
1
CM
29 tháng 12 2017
Xét a + b 8 với mọi a,b ≥ 0 ta có:
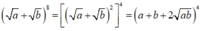
Áp dụng bất đẳng Cô-si cho hai số dương a + b và 2 a b ta được:
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 3 2021
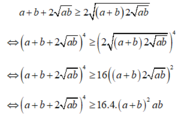
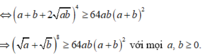
\(\sqrt{\dfrac{a}{b+c}}=\dfrac{a}{\sqrt{a\left(b+c\right)}}\ge\dfrac{2a}{a+b+c}\)
Tương tự: \(\sqrt{\dfrac{b}{c+a}}\ge\dfrac{2b}{a+b+c}\) ; \(\sqrt{\dfrac{c}{a+b}}\ge\dfrac{2c}{a+b+c}\)
Cộng vế:
\(VT\ge\dfrac{2a+2b+2c}{a+b+c}=2\)
Dấu "=" ko xảy ra nên \(VT>2\)
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
Đường thẳng AB có một vectơ chỉ phương là \(\overrightarrow {{u_{AB}}} = \overrightarrow {AB} = \left( { - a;b} \right)\). Do đó \(\overrightarrow {{n_{AB}}} = \left( {b;a} \right)\)
Phương trình tổng quát của đường thẳng AB có vectơ pháp tuyến \(\overrightarrow {{n_{AB}}} = \left( {b;a} \right)\) và đi qua điểm \(A\left( {a;0} \right)\)là: \(b\left( {x - a} \right) + a\left( {y - 0} \right) \Leftrightarrow bx + ay - ab = 0 \Leftrightarrow \frac{x}{a} + \frac{y}{b} = 1\).
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2021
\(VT=\dfrac{a^4}{ab}+\dfrac{b^4}{bc}+\dfrac{c^4}{ca}\ge\dfrac{\left(a^2+b^2+c^2\right)^2}{ab+bc+ca}\ge\dfrac{\left(ab+bc+ca\right)^2}{ab+bc+ca}=ab+bc+ca\)
Dấu "=" xảy ra khi \(a=b=c\)
6 tháng 3 2021
Ta chứng minh bđt phụ \(x^2+y^2+z^2\ge xy+yz+zx\forall x,y,z>0\)
\(\Leftrightarrow2x^2+2y^2+2z^2\ge2xy+2yz+2zx\Leftrightarrow x^2-2xy+y^2+y^2-2yz+z^2+z^2-2zx+x^2\ge0\Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\)\(\Rightarrow x^2+y^2+z^2\ge xy+yz+zx\left(1\right)\)
Áp dụng bđt Cô-si vào các số a,b,c dương :
\(\dfrac{a^3}{b}+ab\ge2\sqrt{\dfrac{a^3}{b}\cdot ab}=2\sqrt{a^4}=2a^2\)
Chứng minh tương tự ta được:
\(\dfrac{b^3}{c}+bc\ge2b^2;\dfrac{c^3}{a}+ca\ge2c^2\)
\(\Rightarrow\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}+ab+bc+ca\ge2a^2+2b^2+2c^2\ge2ab+2bc+2ca\) (do áp dụng (1)) \(\Rightarrow\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}\ge2\left(ab+bc+ca\right)-\left(ab+bc+ca\right)=ab+bc+ca\)
Dấu = xảy ra \(\Leftrightarrow a=b=c\)
TD
1
11 tháng 9 2020
Bằng phản chứng giả sử a và b đều âm
\(\Rightarrow a< 0,b< 0\Rightarrow a+b< 0\)
Mà theo đề: \(a+b>0\)---> Mâu thuẫn giả thiết, vậy có ít nhất 1 trong a,b phải dương
a < b ⇔ a + (-b) < b +(-b) ⇔ a - b < 0