Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: AH vuông BC => ^AHB = 90 độ
Xét trong đường tròn tâm O
^ACB chắn cung AD và AD là đường kính => ^ACB = 90 độ
Xét \(\Delta\)AHB và \(\Delta\)ACD có: ^AHB = ^ACB ( = 90 độ ) ; ^ABH = ^ADC ( cùng chắn cung AC )
=> \(\Delta\)AHB ~ \(\Delta\)ACD (g-g)

a: Xét ΔAIK vuông tại K và ΔBIH vuông tạiH có
góc AIK=góc BIH
=>ΔAIK đồng dạng với ΔBIH
b: Xét ΔAHC vuông tại H và ΔBKC vuông tại K có
góc C chung
=>ΔAHC đồng dạng với ΔBKC
c: Xét (O) có
ΔACD nội tiếp
AD là đường kính
=>ΔACD vuông tại C
=>CD vuông góc AC
=>CD//BI
d: Xét (O) có
ΔABD nội tiếp
AD là đường kính
=>ΔABD vuông tạiB
=>BD//CI
Xét tứ giác BICD có
BI//CD
BD//CI
=>BICD là hình bình hành
e: ΔOBC cân tại O
mà OM là đường cao
nên M là trung điểm của BC
=>M là trung điểm của ID
Xét ΔDAI có
M,O lần lượt là trung điểm của DI.DA
nên MO là đường trung bình
=>MO=1/2AI

Bạn tự vẽ hình nha
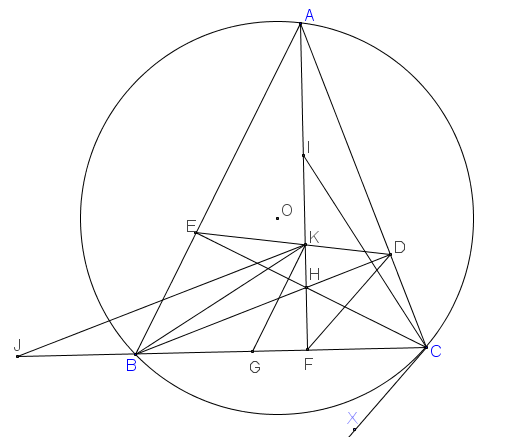
a) Xét \(\Delta\)ABC có:BI,CK là hai đường cao
Mà BI cắt CK tại H(gt)
=> H là trực tâm \(\Delta\)ABC
=>AH cũng là đường cao thứ 3 của \(\Delta\)ABC
Xét \(\Delta\)ABI và \(\Delta\)ACK có:
^AIB=^AKC =90(gt)
^A: góc chung
=> \(\Delta\)ABI ~\(\Delta\)ACK(g.g)
b) xét \(\Delta\)ADC và \(\Delta\)AID có:
^ADC=^AID=90(gt)
^A:góc chung
=> \(\Delta\)ADC~\(\Delta\)AID(g.g)
=>\(\frac{AD}{AI}=\frac{AC}{AD}\)
=> AD^2 =AC*AI

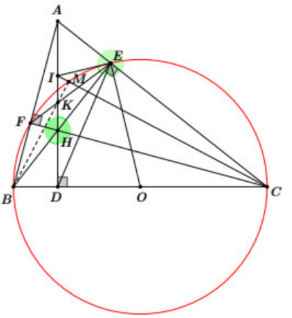
d)
Trên BF lấy điểm G sao cho GK //AB
=>KG⊥⊥CE (1) và BGBF=AKAFBGBF=AKAF (2)
theo câu c), DH là phân giác trong ˆKDFKDF^ (3)
=>HKHF=DKDFHKHF=DKDF (4)
có DA⊥⊥DH (5)
từ (3, 5) =>DA là phân giác ngoài ˆKDFKDF^
=>AKAF=DKDFAKAF=DKDF (6)
từ (2, 4, 6) =>BGBF=HKHFBGBF=HKHF (7)
trên tia đối tia BC lấy điểm J sao cho BJ =BG
=>BJBF=BGBFBJBF=BGBF (8)
từ (7, 8) =>BJBF=HKHFBJBF=HKHF
=>JK // BH
=>JK⊥⊥AC (8)
từ (1, 8) =>ˆJKG=ˆACHJKG^=ACH^ (9)
và có JF⊥⊥AH và (1)=>ˆKGJ=ˆCHAKGJ^=CHA^ (10)
từ (9, 10) =>△KGJ∼△CHA△KGJ∼△CHA (g, g)
=>KGCH=GJHA=2.GB2.HI=GBHIKGCH=GJHA=2.GB2.HI=GBHI (11)
từ (10, 11) =>△KGB∼△CHI△KGB∼△CHI (c, g, c)
=>ˆKBF=ˆCIFKBF^=CIF^
=>△FBK∼△FIC△FBK∼△FIC (đpcm)
và ˆICB+ˆFBKICB^+FBK^
=ˆBKF+ˆFBK=90∘=BKF^+FBK^=90∘
=>BK⊥CIBK⊥CI =>K là trực tâm của tam giác IBC (đpcm)
Hình gửi kèm

vẽ đường tròn ngoại tiếp ngũ giác đều ABCDE
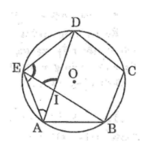

Suy ra tam giác DEI cân tại D ⇒ DI = DE
Mà DE =AE
Nên DI = AE (7)
Từ (4) và (7) suy ra: D I 2 = AI.AD
Xét tứ giác AEDB có: \(\widehat{AEB} = \widehat{ADB} = 90^o \)
⇒ Tứ giác AEDB nội tiếp (2 đỉnh E và D kề nhau cùng nhìn AB dưới 1 cặp góc bằng nhau)
⇒ \(\widehat{EAD} = \widehat{EBD} \) (cùng chắn \(\stackrel\frown{\text{ED}}\))
Xét ΔADC và ΔHDB có:
\(\widehat{ADC} = \widehat{HDB} = 90^o\)
\(\widehat{CAD} = \widehat{HBD} \) (cmt)
⇒ ΔADC ∼ ΔBDH (g-g)
giúp mik vs