PT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
19 tháng 7 2019
Đề a,b bạn ghi mik ko hiểu
c)Ta có : \(x+y=a=>x^2+y^2+2xy=a^2\)
Mà \(x^2+y^2=b\)nên\(b+2xy=a^2=>xy=\frac{a^2-b}{2}\)
\(x^3+y^3=\left(x+y\right)\left(x^2+y^2-xy\right)\)
Thay \(x+y=a\) ; \(x^2+y^2=b\)và \(xy=\frac{a^2-b}{2}\)ta có : \(x^3+y^3=a\left(b-\frac{a^2-b}{2}\right)=ab-\frac{a^3-ab}{2}\)
NT
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7 2024
b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
NH
1
15 tháng 10 2018
Ta có:
\(E=x^3-y^3-36xy\)
\(E=\left(x-y\right)\left(x^2+xy+y^2\right)-36xy\)
\(E=12\left(x^2+xy+y^2\right)-36xy\) ( vì x - y =12 )
\(E=12\left(x^2+y+y^2-3xy\right)\)
\(E=12\left(x^2-2xy+y^2\right)\)
\(E=12\left(x-y\right)^2\)
\(E=12\cdot12^2\) ( vì x - y =12 )
\(E=12^3=1728\)
Hok tốt!
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7 2024
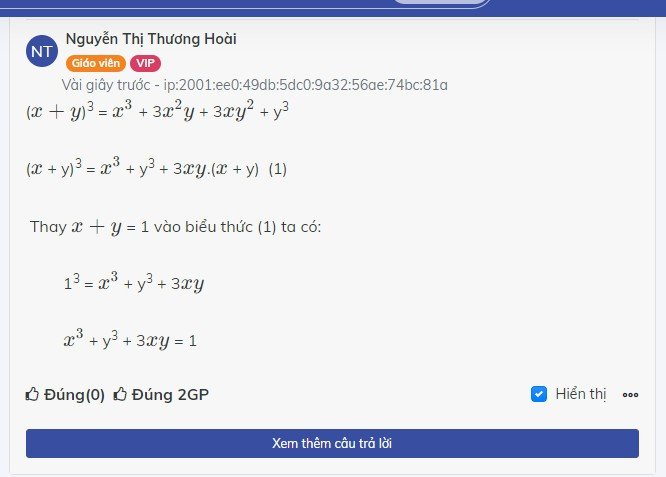
13 = (\(x+y\))3 = \(x^3\) + 3\(x^2\)y + 3\(xy^2\) + y3 = \(x^3\)+y3+3\(xy\)(\(x+y\))
1 = \(x^3\)+y3+3\(xy\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7 2024
13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\)y + 3\(xy\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
T
15 tháng 6 2019
#)Giải :
2)
Đặt \(A=x^3-y^3-36xy\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)-36xy\)
\(=\left(x-y\right)\left[\left(x-y\right)^2+3xy\right]\)
\(=12.12^2+3.12xy-36xy\)
\(=12^3\)
T
15 tháng 6 2019
#)Giải :
1)
Ta có \(x+y=-5\Rightarrow\left(x+y\right)^2=x^2+y^2+2xy=\left(-5\right)^2=25\)
\(\Rightarrow2xy=25-11=14\)
\(\Rightarrow xy=7\)
\(\Rightarrow2xy.xy=2x^2.y^2=14.7=98\)
\(\left(x^2+y^2\right)^2=11^2=121\)
\(\Rightarrow\left(x^4+y^4\right)+98=121\)
\(\Rightarrow x^4+y^4=23\)