Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ∆ vuông ABC và ∆ vuông AED ta có :
AB = AD (gt)
AC = AD (gt)
=> ∆ABC = ∆AED ( 2 cgv)
=> BD = DE
b) Xét ∆ABD có :
BAC = 90°
=> AD\(\perp\)AE
Mà AB = AD (gt)
=> ∆ABD vuông cân tại A
=> BDC = 45°
Chứng minh tương tự ta có :
BCE = 45°
=> BDC = BCE = 45°
Mà 2 góc này ở vị trí so le trong
=> BD//CE

Xét \(\Delta ABC\perp A\)ta có:
AM là trung tuyến ứng cạnh huyền BC
=> AM=BM=CM=41
Xét \(\Delta AHM\perp H\)ta có:
\(HM^2=AM^2-AH^2\left(pytago\right)\)
\(\Rightarrow HM^2=41^2-40^2=81\)
\(\Rightarrow HM=\sqrt{81}=9\)
Ta có: \(\hept{\begin{cases}BH=BM-HM=41-9=32\\CH=CM+HM=41+9=50\end{cases}}\)
Xét \(\Delta ABH,\Delta ABC\)có:
\(\widehat{AHB}=\widehat{CAB}\left(=90^o\right)\)
\(\widehat{B}:chung\)
\(\Rightarrow\Delta ABH\approx\Delta ABC\left(gg\right)\)
\(\Rightarrow\frac{AB}{BH}=\frac{BC}{BA}\Rightarrow BA^2=BH\cdot BC\)
Xét \(\Delta CHA,\Delta CAB\)có:
\(\widehat{CHA}=\widehat{CAB}\left(=90^o\right)\)
\(\widehat{C}:chung\)
\(\Rightarrow\Delta CHA\approx\Delta CAB\left(gg\right)\)
\(\Rightarrow\frac{AC}{CH}=\frac{BC}{AC}\Rightarrow AC^2=CH\cdot BC\)
Ta có:
\(\left(\frac{AB}{BC}\right)^2=\frac{BH\cdot BC}{HC\cdot BC}=\frac{BH}{HC}=\frac{32}{50}=\frac{16}{25}\)
Vậy \(\frac{AB}{BC}=\frac{16}{25}\)
:> hình dễ bn có thể tự vẽ:Đ vì mik ngại :>
Xét t/gABC_|_ A ta có:
AM là trung tuyến ứng vs cạnh huyền BC
=>AM=BM=CM=41
Lại xét t/gAHM_|_H theo định lý pi-ta-go ta có:
HM2=AM2-AH2
=>HM2=412-402=81
=>HM=\(\sqrt{81}\)=9
Ta có:
BH=BM-HM=41-9=32
CH=CM+HM=41+9=50
Xét t/gABH và t/gABC ta có:
^ABH=^ABC=90o
=>^B chung
=>t/gABH~t/gABC(g.g)
=>BA/BH=BC/BA=>BA2=BH.BC
Xét t/gCAB và t/g CHA ta có:
^CAB=^CHA=90o
=>^C chung
=>AC/AH=BC/AC=>AC2=HC.BC
=>(AB/AC)2=BH.BC/HC.BC=32/50=16/25
=> tỉ số hai cạnh góc AB/AC=16/25

Bài làm
~ Tự vẽ hình, đó mik lm = đt nên k vẽ đc hình ~
a) Xét ∆BOA và ∆COK có:
OA = OK ( GT )
GÓC BOA = GÓC COK ( HAI GÓC ĐỐI )
OB = OC ( O LÀ TRUNG ĐIỂN BC )
=> ∆BOA = ∆COK ( c.g.c )
=> AB = KC ( hai cạnh tương ứng )
=> Góc ABC = GÓC KCB ( HAI GÓC TƯƠNG ỨNG )
MÀ hai góc này ở vị trí số le trong.
=> AB // CK
Mà BA | AC
=> CK | AC
Xét ∆ABC và ∆CKA có:
AB = CK ( cmt )
Góc BAC = góc KCA ( đó AB và CK cùng vuông góc với AC )
Cạnh AC chung.
=> ∆ABC = ∆CKA. ( c.g.c )
Bài alfm
Vì tâm giác ABC = tâm giác AKC
=> BC = AK.
Mà AO là trung điểm AK.
=> AO = 1/2 AK
Hay AO = 1/2BC

a) bạn tự vẽ hình nhé
sau khi kẻ, ta có AC=AH+HC=11
mà tam giác ABH vuông tại H
=> theo định lý Pytago => AH^2+BH^2=AB^2
=>BH=căn bậc 2 của 57
cũng theo định lý Pytago
=>BC^2=HC^2+BH^2
=>BC=căn bậc 2 của 66
b) bạn tự vẽ hình tiếp nha
ta có M là trung điểm của tam giác ABC => AM là đường trung tuyến của tam giác ABC vuông tại A
=>AM=MB=MC
theo định lý Pytago =>do tam giác HAM vuông tại H
=>HM^2+HA^2=AM^2
=>HM=9 => HB=MB-MH=32
=>AB^2=AH^2+HB^2 =>AB=căn bậc 2 của 2624
tương tự tính được AC=căn bậc 2 của 4100
=> AC/AB=5/4
CHÚC BẠN HỌC TỐT!!!

Tự vẽ hình
Ta có: AC = AB và góc CAH = BAH (tính chất của Δ cân)
Cách 1: Xét Δ AHB và Δ AHC có:
AB = AC (gt)
BAH = CAH (chứng minh trên)
AH là cạnh chung
Do đó, Δ AHB = Δ AHC (c.g.c)
=>HB=HC
Biết làm mỗi vậy để nghĩ tiếp đã
Học Tốt

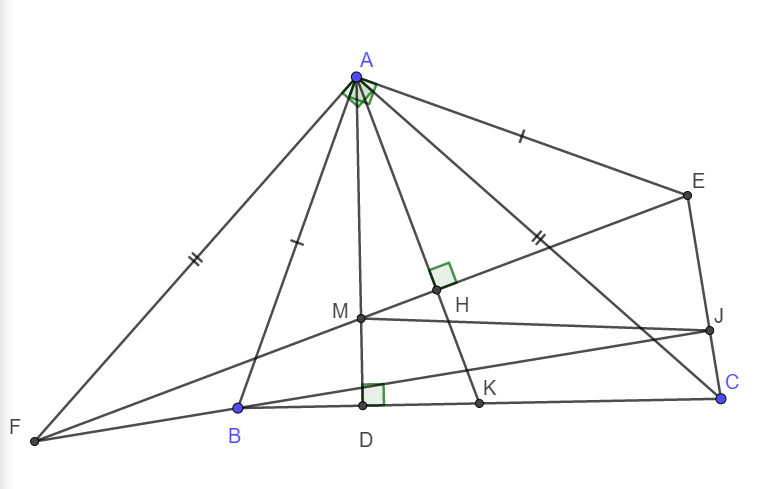
a) Xét tam giác ACK và tam giác FAM có :
AC = FA
\(\widehat{CAK}=\widehat{AFM}\) (Cùng phụ với góc \(\widehat{FAK}\) )
\(\widehat{ACK}=\widehat{FAM}\) (Cùng phụ với góc \(\widehat{DAC}\) )
\(\Rightarrow\Delta ACK=\Delta FAM\left(g-c-g\right)\)
b) Do \(\Delta ACK=\Delta FAM\left(cma\right)\Rightarrow FM=AK\)
Chứng minh hoàn toàn tương tự câu a ta có: \(\Delta ABK=\Delta EAM\left(g-c-g\right)\)
\(\Rightarrow ME=AK\)
Từ đó suy ra FM = ME hay M là trung điểm EF.
c) Kéo dài FB cắt EC tại J. Ta chứng minh \(\widehat{FJE}=90^o\)
Xét tam giác FAB và tam giác CAE có:
FA = CA
AB = AE
\(\widehat{FAB}=\widehat{CAE}\) (Cùng phụ với góc \(\widehat{BAC}\) )
\(\Rightarrow\Delta FAB=\Delta CAE\left(c-g-c\right)\)
\(\Rightarrow FB=CE\) và \(\widehat{AFB}=\widehat{ACE}\)
Xét tứ giác AFJE có:
\(\widehat{AFJ}+\widehat{FJE}+\widehat{JEA}+\widehat{EAF}=360^o\)
\(\Rightarrow\widehat{ACE}+\widehat{FJE}+\widehat{CEA}+\widehat{EAC}+90^o=360^o\)
\(\Rightarrow\widehat{FJE}+\widehat{ACE}+\widehat{CEA}+\widehat{EAC}=270^o\)
\(\Rightarrow\widehat{FJE}+180^o=270^o\)
\(\Rightarrow\widehat{FJE}=90^o\)
Vậy nên \(FB\perp EC\) (đpcm).
Bài 2:
A B C H I M N B' C' D E
a) Gọi giao điểm của đường phân giác ^ABC và ^ACB với AC và AB lần lượt là E và D
Dễ thấy: ^BAH=^ACB (Cùng phụ với ^HAC) => 1/2. ^BAH = 1/2. ^ACB
=> ^DAM=^ACD. Mà ^DAM+^MAC=^BAC=900 => ^ACD+^MAC=900 => AM \(\perp\)CD
hay NI\(\perp\)AM.
Tương tự ta chứng minh MI\(\perp\)AN
Xét tam giác MAN: NI\(\perp\)AM; MI\(\perp\)AN => I là trực tâm của tam giác MAN (đpcm).
b) Do I là trực tâm của tam giác AMN (cmt) => AI\(\perp\)MN hay AI\(\perp\)B'C'
Ta có: Tam giác ABC có 2 đường phân giác ^ABC và ^ACB cắt nhau tại I => AI là phân giác ^BAC
=> AI là phân giác ^B'AC'.
Xét tam giác AB'C': AI là phân giác ^B'AC'. Mà AI\(\perp\)B'C' => Tam giác AB'C' cân tại A
Lại có: ^B'AC'=900 => Tam giác B'AC' vuông cân tại A.