Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

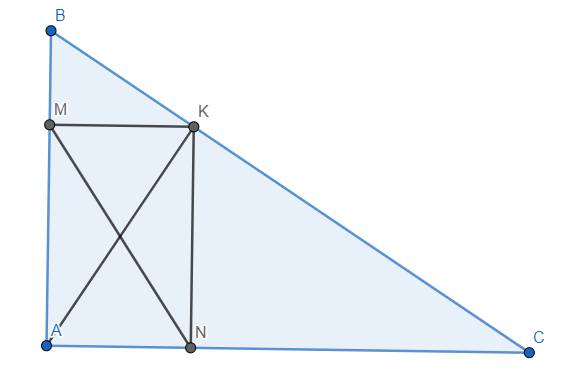
a) Tam giác AKB vuông tại K có đường cao KM nên \(AK^2=AM.AB\)
Chứng minh tương tự, ta có \(AK^2=AN.AC\)
Từ đó suy ra \(AM.AB=AN.AC\) (đpcm)
b) Tam giác KMN vuông tại K nên \(KM^2+KN^2=MN^2\)
Dễ thấy tứ giác AMKN là hình chữ nhật, suy ra \(AK=MN\). Từ đó \(KM^2+KN^2=AK^2\).
Tam giác ABC vuông tại A, đường cao AK nên \(AK^2=KB.KC\)
Thế thì \(KM^2+KN^2=KB.KC\) (đpcm)
c) Tam giác AKB vuông tại K, có đường cao KM nên \(AM.BM=KM^2\)
Tương tự, ta có \(AN.CN=KN^2\)
Từ đó \(AM.BM+AN.CN=KM^2+KN^2\)
Theo câu b), \(KM^2+KN^2=KB.KC\)
Do đó \(AM.BM+AN.CN=KB.KC\) (đpcm)

B H C F N M E
a) \(\hept{\begin{cases}\widehat{HFE}=\widehat{HAE}\\\widehat{HAE}+\widehat{ABH}=90^O\end{cases}\Rightarrow\widehat{HFE}+\widehat{ABH}=90^O}\)
=> \(\widehat{HFE}+\widehat{ABC}=90^O\)(đpcm)
b) AEHF nội tiếp => \(\widehat{AEF}=\widehat{AHF}\)
Mà \(\widehat{AHF}=\widehat{ACB}\)( cùng phụ với \(\widehat{HAC}\))
=> \(\widehat{AEF}=\widehat{ACB}\)
=> BEFC là tứ giác nội tiếp
\(\Rightarrow\hept{\begin{cases}\widehat{EBF}=\widehat{FCE}\\\widehat{BEM}=\widehat{NFC}=90^O\end{cases}\Rightarrow\widehat{EMB}=\widehat{FNC}}\)
\(\Rightarrow\widehat{EMF}=\widehat{ENF}\)
=> EMNF là tứ giác nội tiếp
=> góc ENM = góc EFB
Mà BEFC nội tiếp => góc EFB = góc ECB
Từ 2 điều trên => góc ENM = góc ECB
=> MN // BC => đpcm

a) Ta có MH//AC \(\left(\perp AB\right)\) nên \(\Delta BMH\sim\Delta BAC\)
\(\Rightarrow\dfrac{BM}{BA}=\dfrac{MH}{AC}\) \(\Rightarrow BM.AC=BA.MH\)
Tam giác ABH vuông tại H có đường cao HM
\(BA.MH=HB.HA\)
Tương tự, ta có: \(CN.AB=HC.HA\)
Cộng theo vế 2 hệ thức trên, ta được:
\(BA.MH+CN.AB=HB.HA+HC.HA=HA\left(HB+HC\right)=AH.BC\)
Ta có đpcm.
b) Tam giác ABH vuông tại H có đường cao HM nên \(AM.BM=MH^2\).
Tương tự, ta có \(AN.CN=HN^2\)
Do đó \(VT=AM.BM+AN.CN=MH^2+HN^2\)
Dễ thấy tứ giác AMHN là hình chữ nhật nên \(MH^2+HN^2=MN^2=AH^2\)
Tam giác ABC vuông tại A có đường cao AH nên \(AH^2=BH.CH\)
Từ đó suy ra \(VT=BH.CH=VP\)
Vậy đẳng thức được chứng minh.
c) Xét hệ trục tọa độ Axy với A là gốc tọa độ, \(Ax\equiv AC,Ay\equiv AB\)
Khi đó đặt \(B\left(0;b\right)\), \(C\left(c;0\right)\)
Khi đó phương trình đường thẳng \(BC:y=-\dfrac{b}{c}x+b\)
\(\Rightarrow\) Phương trình đường thẳng \(AH:y=\dfrac{c}{b}x\)
Khi đó hoành độ của điểm H chính là nghiệm của pt hoành độ giao điểm của AH và BC: \(\dfrac{c}{b}x_0=-\dfrac{b}{c}x_0+b\)
\(\Leftrightarrow\left(\dfrac{c}{b}+\dfrac{b}{c}\right)x_0=b\)
\(\Leftrightarrow\left(\dfrac{c^2+b^2}{bc}\right)x_0=b\)
\(\Leftrightarrow x_0=\dfrac{cb^2}{b^2+c^2}\)
\(\Rightarrow y_0=\dfrac{c}{b}x_0=\dfrac{c}{b}.\dfrac{cb^2}{b^2+c^2}=\dfrac{bc^2}{b^2+c^2}\)
Vậy \(H\left(\dfrac{cb^2}{b^2+c^2},\dfrac{bc^2}{b^2+c^2}\right)\)
Vì M là hình chiếu của H lên trục Oy \(\Rightarrow M\left(0,\dfrac{bc^2}{b^2+c^2}\right)\)
Tương tự \(\Rightarrow N\left(\dfrac{cb^2}{b^2+c^2},0\right)\)
Khi đó \(BM=BA-MA=b-\dfrac{bc^2}{b^2+c^2}=\dfrac{b^3+bc^2-bc^2}{b^2+c^2}=\dfrac{b^3}{b^2+c^2}\)
\(CN=CA-NA=c-\dfrac{cb^2}{b^2+c^2}=\dfrac{cb^2+c^3-cb^2}{b^2+c^2}=\dfrac{c^3}{b^2+c^2}\)
\(\Rightarrow\dfrac{BM}{CN}=\dfrac{\dfrac{b^3}{b^2+c^2}}{\dfrac{c^3}{b^2+c^2}}=\dfrac{b^3}{c^3}=\left(\dfrac{b}{c}\right)^3=\left(\dfrac{AB}{AC}\right)^3\)
\(\Rightarrow\sqrt[3]{\dfrac{MB}{NC}}=\dfrac{AB}{AC}\) (đpcm)