Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) D,E lần lượt là điểm chính giữa của cung nhỏ AB, AC
=> \(\hept{\begin{cases}\widebat{AO}=\widebat{BO}\\\widebat{AE}=\widebat{EC}\end{cases}}\)
ta có
\(\widehat{AHK}=\frac{1}{2}\left(\widebat{BO+\widebat{AE}}\right)\)
\(=\frac{1}{2}\left(\widebat{AO}+\widebat{EC}\right)=\widehat{AKH}\)
=> tam giác AHK cân tại A
b) \(\widebat{AD}=\widebat{DB}=>\widehat{AED}=\widehat{BED}\)
\(\widebat{AE=\widebat{EC=>\widehat{ADE}=\widehat{IDE}}}\)
DE cạnh chung
=>\(\Delta ADE=\Delta IDE\left(c-g-c\right)\)
=>\(\hept{\begin{cases}DA=DI\\EA=EI\end{cases}=>DE}\)là đường trung trực của AI
=>\(AI\perp DE\)
c)\(\widehat{EIC}=\frac{1}{2}\left(\widebat{BD}+\widebat{CE}\right)=\frac{1}{2}\left(\widebat{AD}+\widebat{EC}\right)=\widehat{EKC}\)
=> tứ giác EKIC nội tiếp
d) tứ giác EKIC nội tiếp
=>\(\widehat{IKC}=\widehat{BEC}=\widehat{BAC}\)
=>\(IK//AB\)

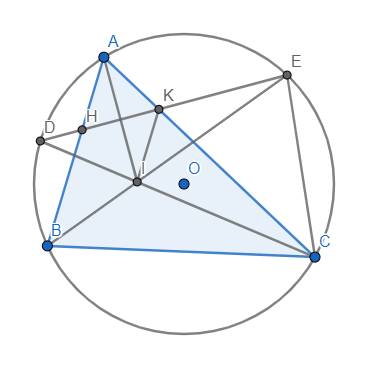
a) Ta có \(\widehat{AHK}=\dfrac{sđ\stackrel\frown{AE}+sđ\stackrel\frown{BD}}{2}\)
và \(\widehat{AKH}=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{AD}}{2}\)
Mặt khác, do D, E lần lượt là điểm chính giữa của cung AB, AC nên \(sđ\stackrel\frown{AD}=sđ\stackrel\frown{BD};sđ\stackrel\frown{AE}=sđ\stackrel\frown{CE}\). Từ đó \(\Rightarrow\widehat{AHK}=\widehat{AKH}\) hay tam giác AHK cân tại A (đpcm).
b) Hiển nhiên I là tâm đường tròn nội tiếp tam giác ABC \(\Rightarrow\) AI là tia phân giác của \(\widehat{BAC}\) (hay chính là \(\widehat{HAK}\)). Mà theo câu a), tam giác AHK cân tại A nên AI đồng thời là đường cao của tam giác AHK \(\Rightarrow AI\perp HK\) hay \(AI\perp DE\) (đpcm)
c) Ta có \(\widehat{CIE}=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{BD}}{2}\)
\(=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{AD}}{2}\) \(=\widehat{CKE}\) nên tứ giác CEKI nội tiếp
\(\Rightarrow\widehat{HKI}=\widehat{DCE}\) \(=\dfrac{sđ\stackrel\frown{DE}}{2}\)
\(=\dfrac{sđ\stackrel\frown{DA}+sđ\stackrel\frown{AE}}{2}\) \(=\dfrac{sđ\stackrel\frown{BD}+sđ\stackrel\frown{AE}}{2}\) \(=\widehat{AHK}\)
Từ đó dễ dàng suy ra KI//AH hay KI//AB (đpcm)

1) góc AKH = 1/2(sđAD + sđEC)
góc AHK = 1/2(sđAE + sđBD)
mà D là điểm chính giữa cung AB
=> cung AD = cung DB
tương tự cung AE = cung EC
từ đó => góc AHK= góc AKH
=> tam giác AKH cân tại A