Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a ) Tứ giác KMIH có \(\widehat{K}=\widehat{I}=\widehat{H}=90^0\Rightarrow\widehat{M_2}=90^0\)
=> Tứ giác KMIH là hình chữ nhật => MK = IH (1)
Ta có : \(\widehat{M_1}+\widehat{M_2}+\widehat{M_3}=180^0\) ( Kề bù ) => \(\widehat{M_1}+\widehat{M_3}=180^0-\widehat{M_2}=180^0-90^0=90^0\)
\(\Rightarrow\widehat{M_1}=90^0-\widehat{M_3}\) (2)
Tam giác IMC vuông tại I => \(\widehat{M_3}+\widehat{C}=90^0\Rightarrow\widehat{C}=90^0-\widehat{M_3}\) (3)
Từ (2) và (3) => \(\widehat{M_1}=\widehat{C}\)
Xét tam giác AKM và tam giác MIC có :
\(\widehat{K}=\widehat{I}=90^0\left(gt\right)\)
AM = MC (gt)
\(\widehat{M_1}=\widehat{C}\left(cmt\right)\)
=> tam giác AKM = tam giác MIC ( CH - GN )
=> IC = MK ( Cạnh tương ứng ) (4)
Từ (1) và (4) => MK = IC = IH (đpcm)
b ) tam giác AHC vuông H
Lại có HM là đường trung tuyến ứng với cạnh huyền là AC
=> \(HM=\frac{1}{2}AC\) ( ĐL đường trung tuyến ứng với cạnh huyền )

1: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
Suy ra: BH=CH
hay H là trung điểm của BC
2: BH=CH=BC/2=6cm
=>AH=8cm
3: Xét ΔAHE có
AK là đường cao
AK là đường trung tuyến
Do đó:ΔAHE cân tại A
hay AH=AE(1)
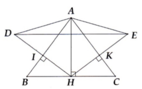
4: Xét ΔADH có
AI là đường cao
AI là đường trung tuyến
Do đó:ΔADH cân tại A
=>AD=AH(2)
Từ (1) và (2)suy ra AD=AE
hay ΔADE cân tại A

a: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
góc HAM=góc KAM
=>ΔAHM=ΔAKM
=>AK=AH
góc BAM+góc CAM=90 độ
góc BMA+góc MAH=90 độ
mà góc CAM=góc HAM
nên góc BAM=góc BMA
=>ΔBAM cân tại B
b: Xét ΔAIC có
CH,IK là đường cao
CH cắt IK tại M
=>M là trực tâm
=>AM vuông góc CI
Xét ΔACI có
AM vừa là đường cao, vừa là phân giác
=>ΔACI cân tại A
Xét ΔAIC có AH/AI=AK/AC
nên KH//IC

a: \(BC^2=7.5^2=56.25\)
\(AB^2+AC^2=4.5^2+6^2=56.25\)
Do đó: \(BC^2=AB^2+AC^2\)
b: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: Xét ΔMHC và ΔMKB có
MH=MK
\(\widehat{HMC}=\widehat{KMB}\)
MC=MB
Do đó: ΔMHC=ΔMKB

a/ Xét tg ADB và tg MDC có
AD=DM (gt) DB=DC (gt)
\(\widehat{ADB}=\widehat{MDC}\)(góc đối đỉnh)
=> tg ADB = tg MDC (c.g.c) => AC=BM
\(\Rightarrow\widehat{CAD}=\widehat{BMD}\)=> AC // BM (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 tạo thành 2 góc so le trong = nhau thì chúng // với nhau)
b/
Xét tg ABM và tg MCA có
tg ABD = tg MCD (cmt) => AB = MC; AC = BM
AM chung
=> tg ABM = tg MCA (c.c.c)
c/
Xét tg vuông ABH và tg vuông MCK có
tg ABD = tg MCD (cmt) => \(\widehat{ABH}=\widehat{MCK}\)
AB=CM (cmt)
=> tg ABH = tg MCK (Hai tg vuông có cạnh huyền và góc nhọn tương ứng = nhau) => BH=CK
Mà BK=BC-CK; CH=BC-BH => BK=CH
d/
Xét tg vuông AHD và tg vuông MKD có
DA=DM (gt); \(\widehat{ADH}=\widehat{MDK}\)(góc đối đỉnh) => tg AHD = tg MKD (Hai tg vuông có cạnh huyền và góc nhọn tương ứng = nhau)
\(\Rightarrow\widehat{DAH}=\widehat{DMK}\) => HM // AK (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 tạo thành 2 góc so le trong = nhau thì chúng // với nhau)

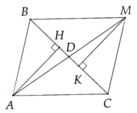



a: Xét ΔAHC có
M là trung điểm của AC
MK//HC
DO đó K là trung điểm của AH
Xét ΔAHC có
M là trung điểm của AC
MI//AH
Do đó:I là trung điểm của HC
Xét ΔABC có
M là trung điểm của AC
K là trung điểm của AH
Do đó: MK là đường trung bình
=>MK=IC=IH
b: ta có: ΔAHC vuông tại H
mà HM là đường trung tuyến
nên HM=AC/2