Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M H K
a,
*Xét tam giác BDM và tam giác CDA, ta có:
AD = MD (đề ra)
BD = CD (đề ra)
góc BDM = góc CDA (hai góc đối đỉnh)
=> tam giác BDM = tam giác CDA (c.g.c)
=> Góc CAD = góc BMD (hai góc tương ứng)
=> AC // BM (hai góc so le trong bằng nhau)
b,
cm trên.
c,
*Xét tam giác AHD và tam giác MKD, ta có:
AD = MD (đề ra)
Góc ADH = góc MDK (hai góc đối đỉnh)
=> Tam giác AHD = tam giác MKD (cạnh huyền góc nhọn)
=> HD = KD (hai cạnh tương ứng)
Ta có:
BK = BD + DK
CH = CD + HD
Mà BD = CD
HD = KD
=> BK = CH (đpcm)
d,
*Xét tam giác AKD và tam giác MHD, ta có:
AD = MD (đề ra)
HD = KD (cm trên)
Góc HDM = góc KDA (hai góc đối đỉnh)
=> Tam giác AKD = tam giác MHD (c.g.c)
=> Góc HMD = góc KAD (hai góc tương ứng)
=> HM // AK (hai góc so le trong bằng nhau)


a) Xét tam giác AMB và tam giác DMC có:
BM = CM (gt)
AM =DM (gt)
\(\widehat{AMB}=\widehat{DMC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMB=\Delta CMD\left(c-g-c\right)\)
b) Do \(\Delta AMB=\Delta CMD\Rightarrow\widehat{BAM}=\widehat{DCM}\)
Chúng lại ở vị trí so le trong nên AB //CD.
c) Xét tam giác AME có MH là đường cao đồng thời trung tuyến nên tam giác AME cân tại M.
Suy ra MA = ME
Lại có MA = MD nên ME = MD.
d) Xét tam giac AED có MA = ME = MD nê tam giác AED vuông tại E.
Suy ra ED // BC
Xét tam giác cân MED có MK là trung tuyến nên đồng thời là đường cao.
Vậy thì \(MK\perp ED\Rightarrow MK\perp BC\)

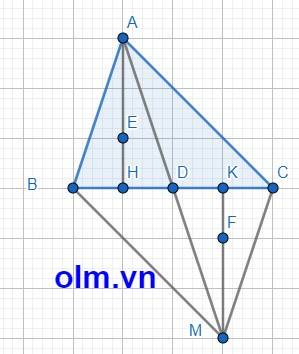
Xét tam giác ACD và tam giác MBD có:
AD = DM (gt)
BD = DC (gt)
\(\widehat{BDM}\) = \(\widehat{ADC}\) (hai góc đối đỉnh)
⇒ \(\Delta\)ACD = \(\Delta\) MBD (c-g-c)
Xét tứ giác ABMC có
AD = DM
BD = DC
⇒ tứ giác ABMC là hình bình hành vì tứ giác có hai đường chéo căt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
⇒ AC // BM
⇒ \(\widehat{ABM}\) = \(\widehat{MCA}\) (vì tứ giác ABMC là hình bình hành)
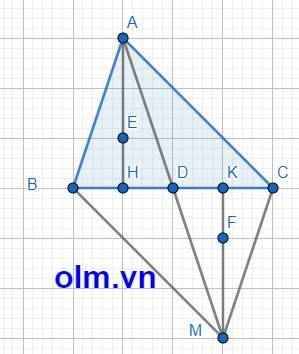
xét tam giác ACD và tam giác MBD có
AD=DM [ gt ]
BD=DC[ gt ]
BDM = ADC hai góc đối đỉnh
suy ra tam giác ACD= tam giác MBD [ c-g-c]
xét tứ giác ABMC có
AD = DM
BD=DC
suy ra tứ giác ABMC là hình bình hành vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành
suy ra ABM=MCA vì tứ giác ABMC là hình bình hành .

a: Xét ΔABD và ΔMCD có
DA=DM
\(\widehat{ADB}=\widehat{MDC}\)
DB=DC
Do đó: ΔABD=ΔMCD
b: Xét ΔAHD vuông tại H và ΔMKD vuông tại K có
DA=DM
\(\widehat{ADH}=\widehat{MDK}\)
Do đó: ΔAHD=ΔMKD
Suy ra: AH=MK

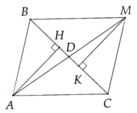
a/ Xét tg ADB và tg MDC có
AD=DM (gt) DB=DC (gt)
\(\widehat{ADB}=\widehat{MDC}\)(góc đối đỉnh)
=> tg ADB = tg MDC (c.g.c) => AC=BM
\(\Rightarrow\widehat{CAD}=\widehat{BMD}\)=> AC // BM (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 tạo thành 2 góc so le trong = nhau thì chúng // với nhau)
b/
Xét tg ABM và tg MCA có
tg ABD = tg MCD (cmt) => AB = MC; AC = BM
AM chung
=> tg ABM = tg MCA (c.c.c)
c/
Xét tg vuông ABH và tg vuông MCK có
tg ABD = tg MCD (cmt) => \(\widehat{ABH}=\widehat{MCK}\)
AB=CM (cmt)
=> tg ABH = tg MCK (Hai tg vuông có cạnh huyền và góc nhọn tương ứng = nhau) => BH=CK
Mà BK=BC-CK; CH=BC-BH => BK=CH
d/
Xét tg vuông AHD và tg vuông MKD có
DA=DM (gt); \(\widehat{ADH}=\widehat{MDK}\)(góc đối đỉnh) => tg AHD = tg MKD (Hai tg vuông có cạnh huyền và góc nhọn tương ứng = nhau)
\(\Rightarrow\widehat{DAH}=\widehat{DMK}\) => HM // AK (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 tạo thành 2 góc so le trong = nhau thì chúng // với nhau)