Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hình vẽ:
a) Vì M là trung điểm của AB nên AM = BM = \(\frac{AB}{2}\)
Xét Δ AMK và Δ BMC có:
AM = BM (cmt)
AMK = BMC (đối đỉnh)
MK = MC (gt)
Do đó, Δ AMK = Δ BMC (c.g.c) (đpcm)
b) Vì N là trung điểm của AC nên AN = NC
Xét Δ ANI và Δ CNB có:
AN = NC (cmt)
ANI = CNB (đối đỉnh)
NI = NB (gt)
Do đó, Δ ANI = Δ CNB (c.g.c)
=> AI = BC (2 cạnh tương ứng) (đpcm)
c) Vì Δ AMK = Δ BMC (câu a) => AKM = MCB (2 góc tương ứng)
Mà AKM và MCB là 2 góc so le trong nên AK // BC (1)
Vì Δ ANI = Δ CNB (câu b) => IAN = NBC (2 góc tương ứng)
Mà IAN và NBC là 2 góc so le trong nên AI // BC (2)
Từ (1) và (2) => AK và AI trùng nhau hay 3 điểm I, A, K thẳng hàng (3)
Có: Δ AMK = Δ BMC (câu a) => AK = BC (2 cạnh tương ứng)
Mà AI = BC (câu b) => AK = AI (4)
Từ (3) và (4) => A là trung điểm của IK (đpcm)

Bài 2
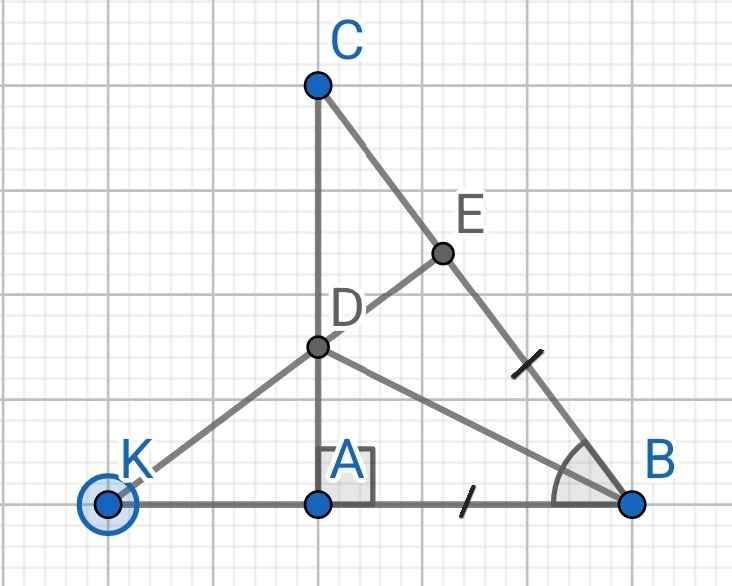
a) Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠EBD
Xét ∆ABD và ∆EBD có:
AB = BE (gt)
∠ABD = ∠EBD (cmt)
BD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED (hai góc tương ứng)
⇒ ∠BED = 90⁰
⇒ DE ⊥ BE
⇒ DE ⊥ BC
c) Do DE ⊥ BC (cmt)
⇒ ∠DEC = 90⁰
⇒ ∆DEC vuông tại E
Do ∆ABD = ∆EBD (cmt)
⇒ AD = DE (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ADK và ∆DEC có:
AD = DE (cmt)
∠ADK = ∠EDC (đối đỉnh)
⇒ ∆ADK = ∆DEC (cạnh góc vuông - góc nhọn kề)
⇒ AK = EC (hai cạnh tương ứng)
Ta có:
AB = BE (gt)
AK = EC (cmt)
⇒ AB + AK = BE + EC
⇒ BK = BC
Bài 1
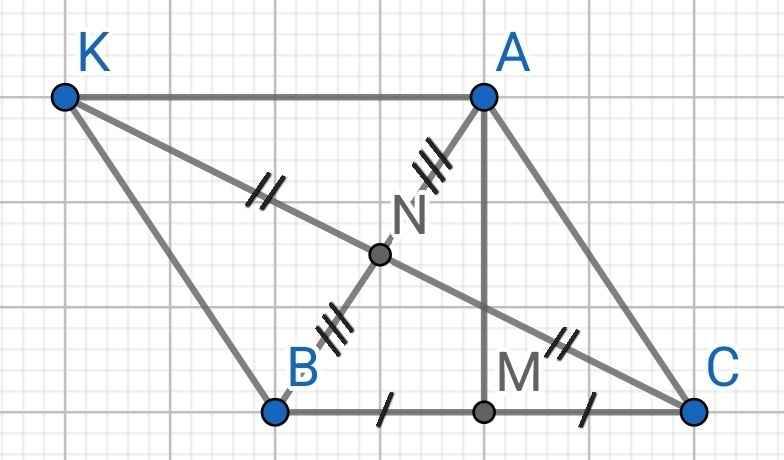 a) Xét ∆ABM và ∆ACM có:
a) Xét ∆ABM và ∆ACM có:
AM là cạnh chung
AB = AC (gt)
MB = MC (gt)
⇒ ∆ABM = ∆ACM (c-c-c)
b) Do M là trung điểm của BC
⇒ BC = 2MC
Xét ∆ANK và ∆BNC có:
AN = BN (gt)
NK = NC (gt)
∠ANK = ∠BNC (đối đỉnh)
⇒ ∆ANK = ∆BNC (c-g-c)
⇒ AK = BC (hai cạnh tương ứng)
Mà BC = 2MC (cmt)
⇒ AK = 2MC
c) Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
⇒ ∆AMB vuông tại M
⇒ ∠ABM + ∠BAM = 90⁰ (1)
Do ∆ANK = ∆BNC (cmt)
⇒ ∠KAN = ∠NBC (hai góc tương ứng)
⇒ ∠KAN = ∠ABM (2)
Từ (1) và (2) ⇒ ∠MAK = ∠KAN + ∠BAM = 90⁰

a: Xét ΔMAB và ΔMDC có
\(\widehat{MBA}=\widehat{MCD}\)(hai góc so le trong, AB//CD)
MB=MC
\(\widehat{AMB}=\widehat{DMC}\)
Do đó: ΔMAB=ΔMDC
=>MA=MD
=>M là trung điểm của AD
b: Sửa đề; NK=NB
Xét tứ giác ABCK có
N là trung điểm chung của AC và BK
=>ABCK là hình bình hành
=>CK=AB
c: ABCK là hình bình hành
=>CK//AB
mà CD//AB
và CD,CK có điểm chung là C
nên K,C,D thẳng hàng

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét tứ giác ANMC có
I là trung điểm của AM
I là trung điểm của CN
Do đó: ANMC là hình bình hành
Suy ra: AN//MC
hay AN//BC
c: Xét tứ giác ABMK có
I là trung điểm của BK
I là trung điểm của AM
Do đó: ABMK là hình bình hành
Suy ra: AK//BM
hay AK//BC
mà AN//BC
và AN,AK có điểm chung là A
nên A,N,K thẳng hàng

Ta có hình vẽ:
Vì CN = 2CI nên CI = IN (đã kí hiệu trên hình)
Vì BK = 2BI nên BI = IK (đã kí hiệu trên hình)
a/ Xét tam giác AMB và tam giác AMC có:
AM: cạnh chung
AB = AC (GT)
BM = MC (GT)
=> tam giác AMB = tam giác AMC (c.c.c)
b/ Xét tam giác IMC và tam giác IAN có:
CI = IN (đã chứng minh đầu bài)
AI = IM (GT)
\(\widehat{AIN}\)=\(\widehat{MIC}\) (đối đỉnh)
=> tam giác IMC = tam giác IAN (c.g.c)
=> \(\widehat{ANI}\)=\(\widehat{ICM}\) (2 góc tương ứng)
Mà 2 góc này đang ở vị trí so le trong
=> AN//BC (đpcm)
c/ Xét tam giác IMB và tam giác IAK có:
BI = IK (đã chứng minh đầu bài)
AI = IM (GT)
\(\widehat{BIM}\)=\(\widehat{KIA}\) (đối đỉnh)
=> tam giác IMB = tam giác IAK (c.g.c)
=> \(\widehat{AKI}\)=\(\widehat{IBM}\)(2 góc tương ứng)
Mà 2 góc này đang ở vị trí so le trong
=> AK//BC
Ta có: AN // BC
AK // BC
=> AN trùng AK
hay N,A,K thẳng hàng

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét tứ giác ANMC có
I là trung điểm của AM
I là trung điểm của NC
Do đó: ANMC là hình bình hành
Suy ra: AN//MC
hay AN//BC
dễ mà
co AI//BC ( cmt)
AK // BC ( cmt )
=>A I K thẳng hàng (tính chất )
ta co AI=BC (cmt)
AK=BC cmt)
=> AI=AK (tính chất bắc cầu)
=> A là tđ của IK