Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hình vẽ:
K A B C M K I N
a) Vì M là trung điểm của AB nên AM = BM = \(\frac{AB}{2}\)
Xét Δ AMK và Δ BMC có:
AM = BM (cmt)
AMK = BMC (đối đỉnh)
MK = MC (gt)
Do đó, Δ AMK = Δ BMC (c.g.c) (đpcm)
b) Vì N là trung điểm của AC nên AN = NC
Xét Δ ANI và Δ CNB có:
AN = NC (cmt)
ANI = CNB (đối đỉnh)
NI = NB (gt)
Do đó, Δ ANI = Δ CNB (c.g.c)
=> AI = BC (2 cạnh tương ứng) (đpcm)
c) Vì Δ AMK = Δ BMC (câu a) => AKM = MCB (2 góc tương ứng)
Mà AKM và MCB là 2 góc so le trong nên AK // BC (1)
Vì Δ ANI = Δ CNB (câu b) => IAN = NBC (2 góc tương ứng)
Mà IAN và NBC là 2 góc so le trong nên AI // BC (2)
Từ (1) và (2) => AK và AI trùng nhau hay 3 điểm I, A, K thẳng hàng (3)
Có: Δ AMK = Δ BMC (câu a) => AK = BC (2 cạnh tương ứng)
Mà AI = BC (câu b) => AK = AI (4)
Từ (3) và (4) => A là trung điểm của IK (đpcm)

a/ Xét tam giác AMI và tam giác BMC có:
AM = MB (GT)
góc AMI = góc BMC (đđ)
MI = MC (GT)
Vậy tam giác AMI = tam giác BMC.
b/ Ta có: tam giác AMI = tam giác BMC
=> AI = BC (hai cạnh tương ứng)
Ta có: tam giác AMI = tam giác BMC
=> góc AIM = góc MCB (hai góc t/ư)
Mà hai góc này ở vị trí slt
=> AI // BC (đpcm).
c/ Xét tam giác AKN và tam giác NBC có:
AN = NC (GT)
góc ANK = góc BNC (đđ)
NK = NB (GT)
Vậy tam giác AKN = tam giác NBC.
=> AK = BC (hai cạnh tương ứng)
Ta có: AI = BC (cmt)
Ta lại có: AK = BC (cmt)
=> AI = AK (t/c bắc cầu).
d/ Ta có: tam giác AKN = tam giác NBC
=> góc AKN = góc NBC (hai góc t/ư)
Mà hai góc này đang ở vị trí slt
=> AK // BC (đpcm).
e/ Ta có: AI // BC (cmt)
Ta lại có: AK // BC (cmt)
==> AI trùng AK
hay A; I; K thẳng hàng.
g/ Ta có: AI = AK (cmt)
và ta lại có: A; I; K thẳng hàng
===> A là trung điểm của IK
----> đpcm.

xét tam giác ame và tam giác bmc
me=mc (gt)
góc ema= góc bmc (đối đỉnh)
am=bm( m là trung điểm của ab)
=> tam giác ame= tam giác bmc(c.g.c)
=> góc eam= góc cbm ( 2 cạnh tương ứng)
mà góc eam và góc cbm SLT
=>ae //bc
xét tam giác afn và tam giác cbn
fn=bn (gt)
góc an f= góc bnc (đ đ)
an=cn ( n là trung điểm của ac)
=> tam giác a fn= tam giác cbn (c.g.c)
=> a f=cb (2 cạnh t ung)
mà ae=cb (tam giác ame= tam giác bmc)
=>a f= ae (=cb)
=> a là trung điểm của e f

a. Xét tam giác AIN và tam giác CBN có:
IN = NB (giả thuyết)
góc ANI = góc CNB (hai góc đối đỉnh)
AN = NC (N là trung điểm của AC)
=> tam giác AIN = tam giác CBN (c.g.c)
=> góc NAI = góc NCB
=> AI // BC (vì có hai góc song le trong bằng nhau)
b. Xét tam giác AMK và tam giác BMC có:
AM = MB (M là trung điểm của AB)
góc AMK = góc BMC (hai góc đối đỉnh)
KM = MC (giả thuyết)
=> tam giác AMK = tam giác BMC (c.g.c)
=> AK = BC (2 cạnh tương ứng) (1)
Mà tam giác ANI = tam giác CNB (cmt)
=> AI = CB (hai cạnh tương ứng) (2)
Từ (1) và (2) => A là trung điểm của đoạn thẳng IK
\(\)

a: Xét tứ giác ABCQ có
N là trung điểm của AC
N là trung điểm của BQ
Do đó: ABCQ là hình bình hành
Suy ra: AQ//BC và AQ=BC
Xét tứ giác ACBP có
M là trung điểm của AB
M là trung điểm của CP
Do đó: ACBP là hình bình hành
Suy ra: AP//BC và AP=BC
Ta có: AQ//BC
AP//BC
mà AQ,AP có điểm chung là A
nên Q,A,P thẳng hàng
mà AP=AQ
nên A là trung điểm của PQ
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=BC/2
hay MN=PQ/4
=>PQ=4MN

tham khảo
mik ko thể vẽ hình đc
SORRY
Giải thích các bước giải:
a.*Xét ΔMBN,ΔMAC có:
MA=MB( vì M là trung điểm BA)
ˆNMB=ˆMC (2 góc đối đỉnh)
MN=MC
⇔ΔMNB=ΔMCA(c.g.c)
⇒ˆMNB=ˆMCA
⇒BN//AC
Vậy BN//AC
b.Từ câu a ⇒AC=BN
Ta có
BN//AC
⇒AC//BE
⇒ˆEAC=ˆAEB
*Xét ΔABE,ΔECA có:
AE chung
ˆAEB=ˆEAC
BE=AC
⇔ ΔABE=ΔECA(c.g.c)
⇒AB=EC
Vậy AB=EC
c.Ta có
AC//BE
⇒ˆACB=ˆCBE
⇒ˆACF=ˆFBE
*Xét ΔACF và ΔBEF có:
FB=FC( F là trung điểm của BC)
ˆACF=ˆEBF
AC=BE
⇔ΔACF=ΔEBF(c.g.c)
⇒ˆAFC=ˆBFE
⇒A,F,E thẳng hàng
Vậy A;F;E thẳng hàng

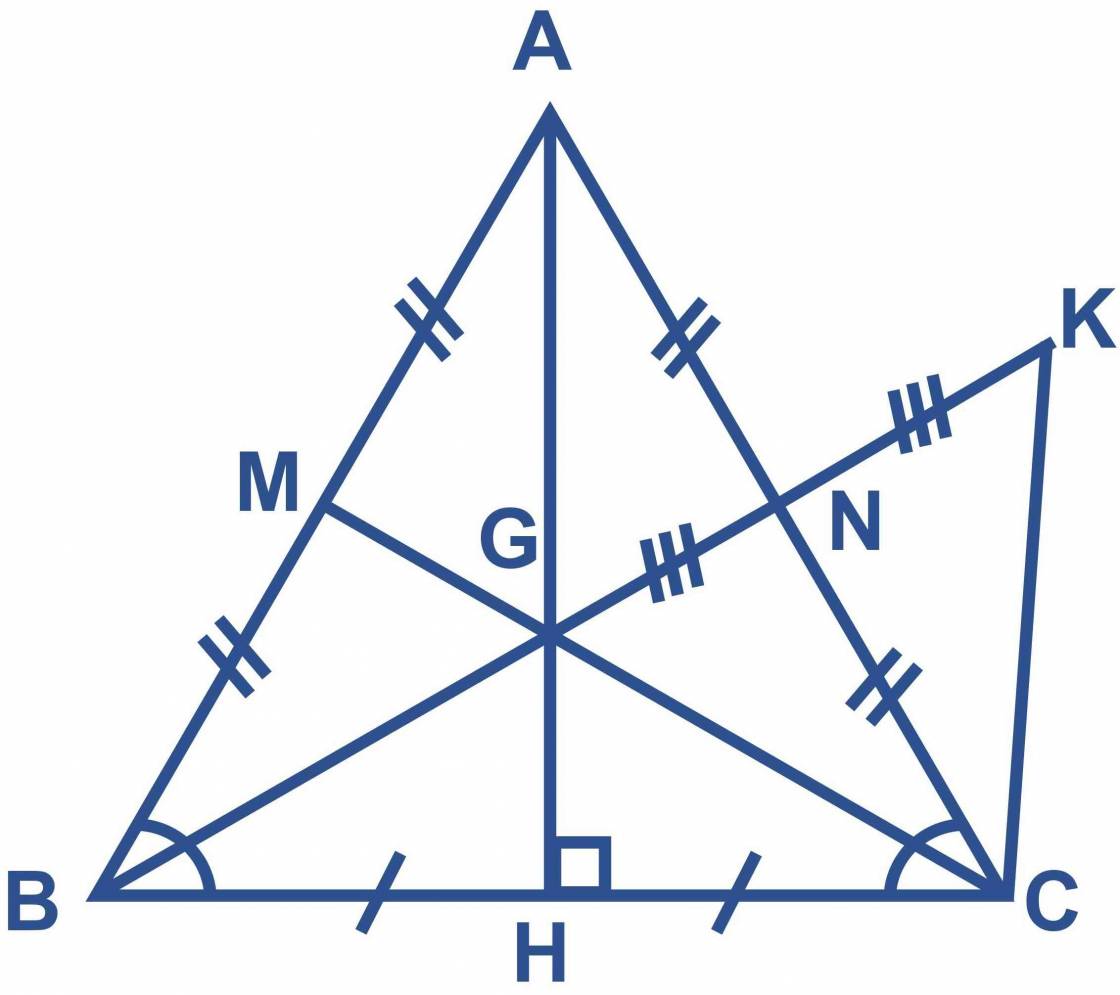
a) trong ΔABC, có góc AHB là góc vuông
góc ABH là góc nhọn
⇒ góc AHB > góc ABH
⇒ AB > AH
b) M là trung điểm của AB và N là trung điểm của AC, mà AB = AC (2 cạnh bên của tam giác cân) ⇒ MB = NC
xét tam giác MBC và tam giác NCB, ta có :
MB = NC (cmt)
góc B = góc C (2 góc đáy của 1 tam giác cân)
BC là cạnh chung
⇒ tam giác MBC = tam giác NCB (c-g-c)
⇒ MC = NB (2 cạnh tương ứng)
c) xét tam giác NAG và tam giác NCK , ta có :
NA = NC (vì N là trung điểm của cạnh AC)
góc NAG = góc NCK (đối đỉnh)
NG = NK (gt)
=> tam giác NAG = tam giác NCK (c-g-c)
=> AG = CK (2 cạnh tương ứng)

a) Xét \(\Delta DNA\) và \(\Delta BCN\), có:
DN = NB (gt)
góc N1 = N2 (2 góc đối đỉnh)
AN = CN (N là TĐ của AC)
->\(\Delta DNA=\Delta BCN\) (c.g.c)
-> AD = BC (2 cạnh tương ứng)
-> góc A1 = góc ACB ( 2 góc tương ứng)
Mà góc A1 và góc ACB là 2 góc SLT
-> AD//BC
Mình chỉ làm được ý a thôi hihi thông cảm

