Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



d: \(SA^2=SB\cdot SC\)
\(SE^2=SB\cdot SC\)
=>SA=SE
Xét ΔOAS và ΔOES có
OA=OE
SA=SE
OS chung
Do đó: ΔOAS=ΔOES
=>\(\widehat{OAS}=\widehat{OES}\)
mà \(\widehat{OAS}=90^0\)
nên \(\widehat{OES}=90^0\)
=>E nằm trên đường tròn đường kính SO
mà S,A,O,D cùng thuộc đường tròn đường kính SO(cmt)
nên E nằm trên đường tròn (SAOD)

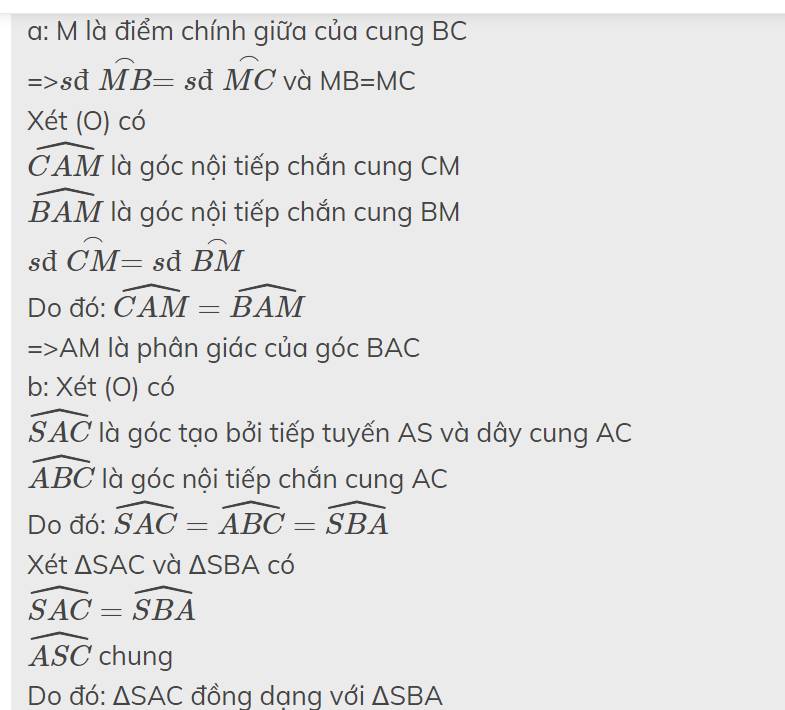
a: M là điểm chính giữa của cung BC
=>\(sđ\stackrel\frown{MB}=sđ\stackrel\frown{MC}\) và MB=MC
Xét (O) có
\(\widehat{CAM}\) là góc nội tiếp chắn cung CM
\(\widehat{BAM}\) là góc nội tiếp chắn cung BM
\(sđ\stackrel\frown{CM}=sđ\stackrel\frown{BM}\)
Do đó: \(\widehat{CAM}=\widehat{BAM}\)
=>AM là phân giác của góc BAC
b: Xét (O) có
\(\widehat{SAC}\) là góc tạo bởi tiếp tuyến AS và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{SAC}=\widehat{ABC}=\widehat{SBA}\)
Xét ΔSAC và ΔSBA có
\(\widehat{SAC}=\widehat{SBA}\)
\(\widehat{ASC}\) chung
Do đó: ΔSAC đồng dạng với ΔSBA
=>\(\dfrac{SA}{SB}=\dfrac{SC}{SA}\)
=>\(SA^2=SB\cdot SC\)
c: Xét (O) có
góc CKA là góc có đỉnh ở trong đường tròn chắn cung AC và BM
=>\(\widehat{CKA}=\dfrac{1}{2}\left(sđ\stackrel\frown{AC}+sđ\stackrel\frown{BM}\right)\)
=>\(\widehat{SKA}=\dfrac{1}{2}\left(sđ\stackrel\frown{AC}+sđ\stackrel\frown{CM}\right)=\dfrac{1}{2}\cdot sđ\stackrel\frown{AM}\)
mà \(\widehat{SAK}=\dfrac{1}{2}\cdot sđ\stackrel\frown{AM}\)(góc tạo bởi tiếp tuyến SA và dây cung AM)
nên \(\widehat{SAK}=\widehat{SKA}\)
=>SA=SK
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(1)
Ta có: MB=MC
=>M nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OM là đường trung trực của BC
=>OM\(\perp\)BC tại D
Xét tứ giác SAOD có
\(\widehat{SAO}+\widehat{SDO}=90^0+90^0=180^0\)
nên SAOD là tứ giác nội tiếp
=>S,A,D,O cùng thuộc một đường tròn

a, Xét tứ giác CDME có
^MEC = ^MDC = 900
mà 2 góc này kề, cùng nhìn cạnh MC
Vậy tứ giác CDME là tứ giác nt 1 đường tròn
b, bạn ktra lại đề
a) Ta có : \(\widehat{O_1}=2\widehat{C}=120^0\) (góc ở tâm gấp đôi góc nội tiếp cùng chắn cung nhỏ AB) nên độ dài cung nhỏ AB là \(\frac{2R\pi.120}{360}=\frac{2}{3}R\pi\)
b) \(\Delta AMC\)cân tại M (MC = MA) có \(\widehat{C}=60^0\)nên \(\Delta AMC\)đều\(\Rightarrow\widehat{AMC}=60^0\Rightarrow\widehat{M_1}=120^0\)
\(\Delta AOK,\Delta BMK\)có \(\widehat{K_1}=\widehat{K_2}\)(đối đỉnh) ; \(\widehat{O_1}=\widehat{M_1}=120^0\Rightarrow\Delta AOK\infty\Delta BMK\left(g-g\right)\)
\(\Rightarrow\frac{AO}{OK}=\frac{BM}{MK}\Rightarrow MK.AO=OK.MB\)
c) Tứ giác ABMO có \(\widehat{O_1}=\widehat{M_1}\)(2 đỉnh kề nhau A,M nhìn xuống cạnh đối diện dưới AB các góc bằng nhau)
=> Tứ giác ABMO nội tiếp hay B,M,O,A cùng thuộc 1 đường tròn