Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: AB < AC (gt)
Suy ra: HB < HC (đường xiên lớn hơn thì hình chiếu lớn hơn)
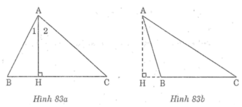
* Trường hợp Bnhọn (hình 83a)
Trong Δ ABC, ta có: AB < AC
Suy ra: ∠B > ∠C(đối diện với cạnh lớn hơn là góc lớn hơn)
Trong Δ AHB, ta có ∠(AHB) = 90o
Suy ra: ∠B + ∠(HAB) = 90o (tính chất tam giác vuông) (1)
Trong Δ AHC, ta có ∠(AHC) = 90o
Suy ra: ∠C + ∠(HAC) = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B + ∠(HAB) = ∠C + ∠(HAC)
Mà ∠B > ∠C nên ∠(HAB) < ∠(HAC)
* Trường hợp Btù (hình 83b)
Vì điểm B nằm giữa H và C nên ∠(HAC) = ∠(HAB) + ∠(BAC)
Vậy ∠(HAB) < ∠(HAC).

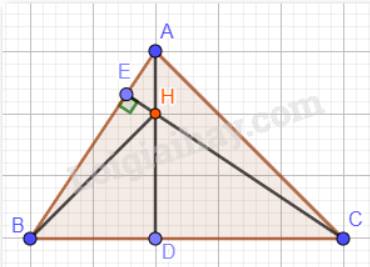
Ta có: AB < AC nên \(\widehat {ACB} < \widehat {ABC}\) (góc ACB đối diện với cạnh AB; góc ABC đối diện với cạnh AC)
Mà tam giác ADB và tam giác ADC vuông tại D.
Vì tổng hai góc nhọn trong một tam giác vuông bằng 90°.
Mà \(\widehat {ACB} < \widehat {ABC}\).
Suy ra: \(90^\circ - \widehat {ACB} > 90^0 - \widehat {ABC}\) hay \(\widehat {DAC} > \widehat {DAB}\).
Vậy \(\widehat {HAC} > \widehat {HAB}\) hay \(\widehat {HAB} < \widehat {HAC}\).
Suy ra: A, B, D sai.
Đáp án: C.\(\widehat {HAB} = \widehat {HCB}\).