Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Ta có: \(\widehat{HAB}+\widehat{HAD}=\widehat{BAD}\)
\(\widehat{HAC}-\widehat{HAD}=\widehat{DAC}\)
Vì AD là tia phân giác của góc BAC => \(\widehat{BAD}=\widehat{DAC}\) =.> ĐPCM
b. Xét tam giác HAC có \(\widehat{AHC}+\widehat{HCA}+\widehat{HAC}=180\text{đ}\text{ộ}\)
=>\(\widehat{HAC}=180^o-\widehat{AHC}-\widehat{HCA}\)
Xét tam giác HAB có \(\widehat{HAB}+\widehat{ABH}+\widehat{BHA}=180^o\)
=> \(\widehat{HAB}=180^o-\widehat{ABH}-\widehat{BHA}\)
Ta có: \(\widehat{HAC}-\widehat{HAB}=180^o-\widehat{AHC}-\widehat{HAC}-\left(180^o-\widehat{ABH}-\widehat{BHA}\right)\)
\(=180^o-90^o-\widehat{HCA}-180^o+\widehat{ABH}+90^o\)
\(=180^o-180^o+90^o-90^o+\widehat{ABH}-\widehat{HCA}\)
\(=\widehat{ABH}-\widehat{HCA}=>\text{Đ}PCM\)
c. Ta có: \(\dfrac{1}{2}\left(\widehat{ABC}-\widehat{ACB}\right)=\dfrac{\widehat{ABC}-\widehat{ACB}}{2}=\dfrac{\widehat{HAC}-\widehat{HAB}}{2}\)
\(=\dfrac{2\widehat{DAH}}{2}=\widehat{DAH}=>\text{Đ}pcm\)

b: Vì góc ABC là góc ngoài cua ΔAHB
nên góc ABC=góc AHB+góc HAB=90 độ+góc HAB
Xét ΔHAC vuông tại H có góc HAC+góc ACB=90 độ
=>góc ACB=90 độ-góc HAC
c: 1/2(góc ABC-góc ACB)
=1/2(180 độ-góc ABH-90 độ+góc HAC)
=1/2(90 độ-góc ABH+góc HAC)
=góc DAH

Ai hack nick mình thì trả lại đi !!!
nick :
- Tên: Vô danh
- Đang học tại: Trường Tiểu học Số 1 Nà Nhạn
- Địa chỉ: Huyện Điện Biên - Điện Biên
- Điểm hỏi đáp: 112SP, 0GP
- Điểm hỏi đáp tuần này: 47SP, 0GP
- Thống kê hỏi đáp
Ai hack hộ mình rồi gửi cho mình nhé mình cảm ơn
Ai là bạn của mình chắn chắn biết nên vào phần bạn bè hỏi mình mới là chủ nick
Mong olm xem xét ko cho ai hack nick nhau nữa ạ! Xin chân thành cảm ơn !
LInk : https://olm.vn/thanhvien/lehoangngantoanhoc

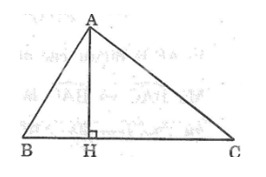
Trong ΔABC ta có ∠AC > ∠AB (gt)
Suy ra: ∠B > ∠C (đối diện cạnh lớn hơn là góc lớn hơn)
Trong ΔAHB có ∠(AHB) = 90o
Suy ra: ∠B + ∠(HAB) = 90o (tính chất tam giác vuông) (1)
Trong ΔAHC có ∠(AHC) = 90o
Suy ra: ∠C + ∠(HAC) = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B + ∠(HAB) = ∠C + ∠(HAC)
Mà ∠B > ∠C nên ∠(HAB) < ∠(HAC) .

Ta có: AB < AC (gt)
Suy ra: HB < HC (đường xiên lớn hơn thì hình chiếu lớn hơn)
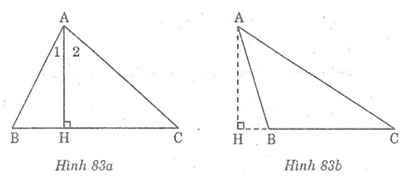
* Trường hợp góc B nhọn
Trong Δ ABC, ta có: AB < AC
Suy ra: góc B > góc C(đối diện với cạnh lớn hơn là góc lớn hơn)
Trong Δ AHB, ta có góc AHB = \(90^0\)
Suy ra: góc B + góc HAB = \(90^0\) (tính chất tam giác vuông) (1)
Trong Δ AHC, ta có góc AHC = \(90^0\)
Suy ra: góc C + góc HAC = \(90^0\) (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: góc B + góc HAB) = góc C + góc HAC
Mà góc B > góc C nên góc HAB < góc HAC
* Trường hợp Btù
Vì điểm B nằm giữa H và C nên góc HAC = góc HAB + góc BAC
Vậy góc HAB < góc HAC.

a) Góc A = 1
Góc B = 3
Góc C = 5
Học tốt!!!
Ta có: AB < AC nên \(\widehat {ACB} < \widehat {ABC}\) (góc ACB đối diện với cạnh AB; góc ABC đối diện với cạnh AC)
Mà tam giác ADB và tam giác ADC vuông tại D.
Vì tổng hai góc nhọn trong một tam giác vuông bằng 90°.
Mà \(\widehat {ACB} < \widehat {ABC}\).
Suy ra: \(90^\circ - \widehat {ACB} > 90^0 - \widehat {ABC}\) hay \(\widehat {DAC} > \widehat {DAB}\).
Vậy \(\widehat {HAC} > \widehat {HAB}\) hay \(\widehat {HAB} < \widehat {HAC}\).
Suy ra: A, B, D sai.
Đáp án: C.\(\widehat {HAB} = \widehat {HCB}\).