Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

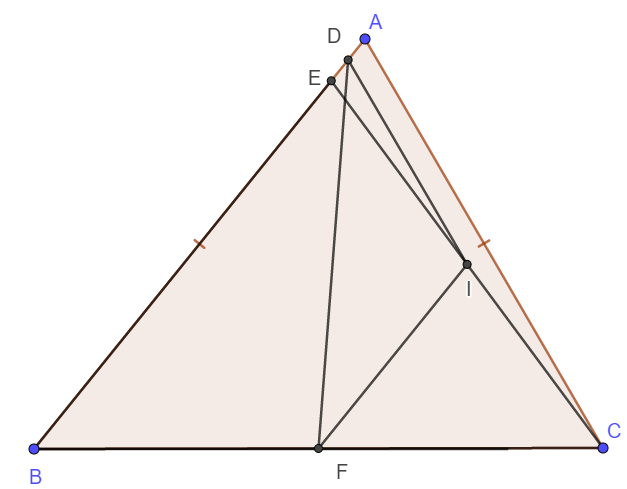
a: Xét ΔEBC có
I là trung điểm của EC
F là trung điểm của BC
Do đó: IF là đường trung bình của ΔEBC
Suy ra: \(IF=\dfrac{EB}{2}\left(1\right)\)
Xét ΔAEC có
I là trung điểm của EC
D là trung điểm của AE
Do đó: ID là đường trung bình của ΔAEC
Suy ra: \(ID=\dfrac{AC}{2}\left(2\right)\)
Từ (1) và (2) suy ra IF=ID
hay ΔIDF cân tại I

gợi ý câu a: dùng tính chất đường trung bình ta được (tự nêu 2 cặp bằng nhau)
ID là đường trung bình trong tam giác ACE \(\RightarrowÌF=AC\left(1\right)\)
IF là đường trung bình tronng tam giác CEB \(\Rightarrow IF=EB\left(2\right)\)
Mà \(AC=EB\left(3\right)\)
Từ (1),(2),(3) \(\Rightarrow ID=IF\)
Suy ra tam giác IDF cân tại I
câu b chưa làm đc

I THUỘC CE mình quên chưa về vào hinh A) CHỨng minh DEC=FEC=>Ei là phân giác=>ID=IF(1diem thuộc tia phân giác thì cách đều 2 cánh)=>IDF cân
b)chứng minh AC// ĐI=>BAC=EDI=IDF+FDE SAU ĐÓ CHỨNG MINH IDF=FDE THẾ LA XONG
A B C E D F I

2)
a/ có M là trung điểm BC
N là trung điểm AD
=> MN//AB//DC ( Tính chất đường trung bình)
=> MN vuông AD
Xét tam giác MAD có
MN vừa là đường trung tuyến ( N là trung điểm AD) vùa là đường trung trực ( N là trung điểm AD và MN vuông AD)
=> tam giác MAD cân tại M
b/ Ta có tam giác MAD cân tại M => góc MAD =góc MDA (1)
ta có GÓC MAB+ GÓC MAD = 90 ĐỘ(2)
GÓC MDA +GÓC MDC =90ĐỘ (3)
(1) (2) (3) => GÓC MAB = GÓC MDC
* Chúc bạn học tốt!

Em tham khảo tại đây nhé.
Câu hỏi của Trần Nam Anh - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
Câu hỏi của Trần Nam Anh - Toán lớp 8 - Học toán với OnlineMath

Xét ΔEAC có
D là trung điểm của AE
I là trung điểm của CE
Do đó: DI là đường trung bình
=>DI//AC và DI=AC/2
Xét ΔEBC có
F là trung điểm của BC
I là trung điểm của EC
Do đó: FI là đường trung bình
=>FI//EB và FI=EB/2
Ta có: FI=EB/2
DI=AC/2
mà EB=AC
nên IF=ID
hay ΔIFD cân tại I
=>\(\widehat{IFD}=\widehat{IDF}\)
mà \(\widehat{DFI}=\widehat{FDB}\)(FI//AB)
nên \(\widehat{FDI}=\widehat{FDB}\)
\(\Leftrightarrow\widehat{BDI}=2\cdot\widehat{IDF}\)
hay \(\widehat{BAC}=2\cdot\widehat{IDF}\)

a) Xét tam giác ECB có I, F lần lượt là trung điểm của CE và CB nên IF là đường trung bình tam giác.
Suy ra \(IF=\frac{ED}{2}\)
Xét tam giác ECA có I, D lần lượt là trung điểm của CE và EA nên ID là đường trung bình tam giác.
Suy ra \(ID=\frac{AC}{2}\)
Mà AC = BE nên ID = IF
Vậy tam giác DIF cân tại I.
b) Do tam giác DIF cân tại I nên \(\widehat{FDI}=\widehat{DFI}\)
Lại có IF là đường trung bình tam giác BEC nên IF // AB, suy ra \(\widehat{DFI}=\widehat{FDB}\)
Từ đó ta có: \(\widehat{FDI}=\widehat{FDB}\Rightarrow\widehat{BDI}=2\widehat{IDF}\)
Cũng do DI là đường trung bình nên DI // AC hay \(\widehat{BDI}=\widehat{BAC}\)
Vậy nên \(\widehat{BAC}=2\widehat{IDF}\)

Sửa đề: D là trung điểm của AE
Xét ΔEAC có
D là trung điểm của AE
I là trung điểm của CE
Do đó: DI là đường trung bình
=>DI//AC và DI=AC/2
Xét ΔEBC có
F là trung điểm của BC
I là trung điểm của EC
Do đó: FI là đường trung bình
=>FI//EB và FI=EB/2
Ta có: FI=EB/2
DI=AC/2
mà EB=AC
nên IF=ID
hay ΔIFD cân tại I
=>\(\widehat{IFD}=\widehat{IDF}\)
mà \(\widehat{DFI}=\widehat{FDB}\)(FI//AB)
nên \(\widehat{FDI}=\widehat{FDB}\)
\(\Leftrightarrow\widehat{BDI}=2\cdot\widehat{IDF}\)
hay \(\widehat{BAC}=2\cdot\widehat{IDF}\)

Em tham khảo tại đây nhé.
Câu hỏi của Trần Nam Anh - Toán lớp 8 - Học toán với OnlineMath
thôi em ko tl lớp6