Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tham khảo tại đây nhé.
Câu hỏi của Trần Nam Anh - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
Câu hỏi của Trần Nam Anh - Toán lớp 8 - Học toán với OnlineMath

Sửa đề: D là trung điểm của AE
Xét ΔEAC có
D là trung điểm của AE
I là trung điểm của CE
Do đó: DI là đường trung bình
=>DI//AC và DI=AC/2
Xét ΔEBC có
F là trung điểm của BC
I là trung điểm của EC
Do đó: FI là đường trung bình
=>FI//EB và FI=EB/2
Ta có: FI=EB/2
DI=AC/2
mà EB=AC
nên IF=ID
hay ΔIFD cân tại I
=>\(\widehat{IFD}=\widehat{IDF}\)
mà \(\widehat{DFI}=\widehat{FDB}\)(FI//AB)
nên \(\widehat{FDI}=\widehat{FDB}\)
\(\Leftrightarrow\widehat{BDI}=2\cdot\widehat{IDF}\)
hay \(\widehat{BAC}=2\cdot\widehat{IDF}\)

Em tham khảo tại đây nhé.
Câu hỏi của Trần Nam Anh - Toán lớp 8 - Học toán với OnlineMath

gợi ý câu a: dùng tính chất đường trung bình ta được (tự nêu 2 cặp bằng nhau)
ID là đường trung bình trong tam giác ACE \(\RightarrowÌF=AC\left(1\right)\)
IF là đường trung bình tronng tam giác CEB \(\Rightarrow IF=EB\left(2\right)\)
Mà \(AC=EB\left(3\right)\)
Từ (1),(2),(3) \(\Rightarrow ID=IF\)
Suy ra tam giác IDF cân tại I
câu b chưa làm đc

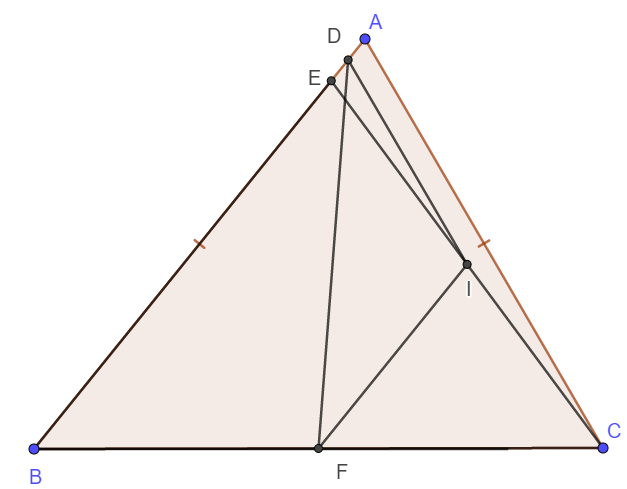
a) Xét tam giác ECB có I, F lần lượt là trung điểm của CE và CB nên IF là đường trung bình tam giác.
Suy ra \(IF=\frac{ED}{2}\)
Xét tam giác ECA có I, D lần lượt là trung điểm của CE và EA nên ID là đường trung bình tam giác.
Suy ra \(ID=\frac{AC}{2}\)
Mà AC = BE nên ID = IF
Vậy tam giác DIF cân tại I.
b) Do tam giác DIF cân tại I nên \(\widehat{FDI}=\widehat{DFI}\)
Lại có IF là đường trung bình tam giác BEC nên IF // AB, suy ra \(\widehat{DFI}=\widehat{FDB}\)
Từ đó ta có: \(\widehat{FDI}=\widehat{FDB}\Rightarrow\widehat{BDI}=2\widehat{IDF}\)
Cũng do DI là đường trung bình nên DI // AC hay \(\widehat{BDI}=\widehat{BAC}\)
Vậy nên \(\widehat{BAC}=2\widehat{IDF}\)

a: Xét ΔEBC có
I là trung điểm của EC
F là trung điểm của BC
Do đó: IF là đường trung bình của ΔEBC
Suy ra: \(IF=\dfrac{EB}{2}\left(1\right)\)
Xét ΔAEC có
I là trung điểm của EC
D là trung điểm của AE
Do đó: ID là đường trung bình của ΔAEC
Suy ra: \(ID=\dfrac{AC}{2}\left(2\right)\)
Từ (1) và (2) suy ra IF=ID
hay ΔIDF cân tại I

2)
a/ có M là trung điểm BC
N là trung điểm AD
=> MN//AB//DC ( Tính chất đường trung bình)
=> MN vuông AD
Xét tam giác MAD có
MN vừa là đường trung tuyến ( N là trung điểm AD) vùa là đường trung trực ( N là trung điểm AD và MN vuông AD)
=> tam giác MAD cân tại M
b/ Ta có tam giác MAD cân tại M => góc MAD =góc MDA (1)
ta có GÓC MAB+ GÓC MAD = 90 ĐỘ(2)
GÓC MDA +GÓC MDC =90ĐỘ (3)
(1) (2) (3) => GÓC MAB = GÓC MDC
* Chúc bạn học tốt!

Xét ΔEAC có
D là trung điểm của AE
I là trung điểm của CE
Do đó: DI là đường trung bình
=>DI//AC và DI=AC/2
Xét ΔEBC có
F là trung điểm của BC
I là trung điểm của EC
Do đó: FI là đường trung bình
=>FI//EB và FI=EB/2
Ta có: FI=EB/2
DI=AC/2
mà EB=AC
nên IF=ID
hay ΔIFD cân tại I
=>\(\widehat{IFD}=\widehat{IDF}\)
mà \(\widehat{DFI}=\widehat{FDB}\)(FI//AB)
nên \(\widehat{FDI}=\widehat{FDB}\)
\(\Leftrightarrow\widehat{BDI}=2\cdot\widehat{IDF}\)
hay \(\widehat{BAC}=2\cdot\widehat{IDF}\)

Xét ΔEAC có
D là trung điểm của AE
I là trung điểm của CE
Do đó: DI là đường trung bình
=>DI//AC và DI=AC/2
Xét ΔEBC có
F là trung điểm của BC
I là trung điểm của EC
Do đó: FI là đường trung bình
=>FI//EB và FI=EB/2
Ta có: FI=EB/2
DI=AC/2
mà EB=AC
nên IF=ID
hay ΔIFD cân tại I
=>\(\widehat{IFD}=\widehat{IDF}\)
mà \(\widehat{DFI}=\widehat{FDB}\)(FI//AB)
nên \(\widehat{FDI}=\widehat{FDB}\)
\(\Leftrightarrow\widehat{BDI}=2\cdot\widehat{IDF}\)
hay \(\widehat{BAC}=2\cdot\widehat{IDF}\)
I THUỘC CE mình quên chưa về vào hinh A) CHỨng minh DEC=FEC=>Ei là phân giác=>ID=IF(1diem thuộc tia phân giác thì cách đều 2 cánh)=>IDF cân
b)chứng minh AC// ĐI=>BAC=EDI=IDF+FDE SAU ĐÓ CHỨNG MINH IDF=FDE THẾ LA XONG
A B C E D F I