Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ 
ab = 8a(b – a)
ab = 8ab – 8a2
8a2 = 7ab
8a = 7b hay

Đầu tiên, cần chứng minh \(\frac{k}{k+1}\) là phân số tối giản với k là số tự nhiên. Thật vậy , gọi ƯCLN(k,k+1) = d (\(d\ge1\))
\(\begin{cases}k⋮d\\k+1⋮d\end{cases}\) => (k+1)-k\(⋮d\) => \(1⋮d\Rightarrow d\le1\)
Mà \(d\ge1\) => d = 1
Vậy \(\frac{k}{k+1}\) là phân số tối giản.
Áp dụng : Đặt \(k=\frac{a}{b}\) , khi đó ta có : \(\frac{1}{k}+1=\frac{b}{a}+1=\frac{a+b}{a}\Rightarrow\frac{a}{a+b}=\frac{k}{k+1}\) là p/s tối giản.
Do a/b tối giản => ƯCLN (a,b) = 1
Mà \(\frac{a}{a+b}=\frac{1}{b}\) (do tính chất loại bỏ)
Tử số là 1 => 1/b tối giản
Vậy a/a + b tối giản

\(\frac{a}{b}\)toi gian khi a khong chia het cho b va b khong chia het cho b
mà a chia hết cho a, a không chia hết cho b suy ra a không chia hết cho a+b
nên a phần a+b tối giản
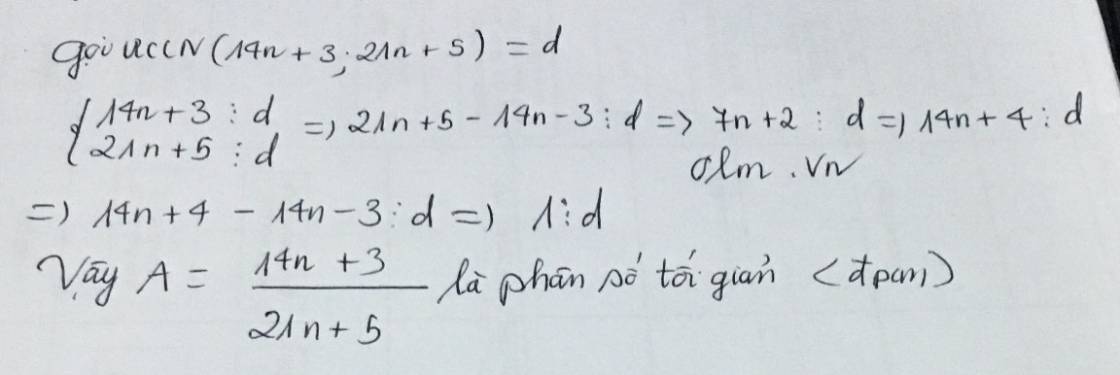
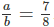
Gọi ƯCLN\(\left(a,a+b\right)=d\) (d \(\in\)N*)
\(\Rightarrow\) a \(⋮\)d ; a+b \(⋮\)d
\(\Rightarrow\) a \(⋮\)d ; b\(⋮\)d
Vì \(\dfrac{a}{b}\)tối giản nên \(\Rightarrow\) d= 1
Vậy nếu \(\dfrac{a}{b}\) tối giản thì \(\dfrac{a}{a+b}\) tối giản