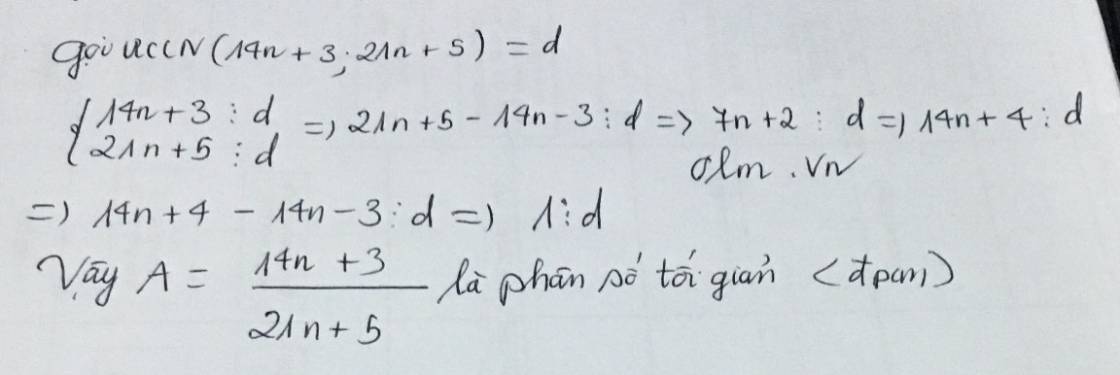Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi d là UCLN(14n+3;21n+4)
ta có:
3(14n+3)-2(21n+4) chia hết cho d
=>(42n+9)-(42n+8) chia hết cho d
=>1 chia hết cho d
=>d=1
=>ps trên tối giản
goỊ Đ LÀ ƯC(21N+4/14N+3
=>14N+3 CHIA HẾT CHO Đ=>3(14N+12)CHIA HẾT CHO Đ
=>21N+4 CHIA HẾT CHO Đ=>2(21+8) CHI HẾT CHO Đ
=>42N+12 -42N+8 CHIA HẾT CHO Đ
=>1 CHIA HẾT CHO Đ =>Đ=1
VÌ 12N+4/14N+3 CÓ ƯC =1
=>21N+4/14N+3 LÀ PHÂN SỐ TỐI GIẢN

Gọi d là ƯC (21n+1; 14n+3)
\(\Rightarrow\)21n+1 chia hết cho d
14n+3 chia hết cho d
\(\Rightarrow\frac{2\left(21n+1\right)}{3\left(14n+3\right)}=\frac{42n+2}{42n+9}\)chia hết cho d
\(\Rightarrow\left(42n+9\right)-\left(42n+2\right)=7\)chia hết cho d
\(\Rightarrow\) Đề viết sai. Không thể chứng minh được vì d phải =1

Gọi ƯCLN (14n + 3 ; 21n + 5) = d
=> 14n + 3 chia hết cho d => 3(14n + 3) chia hết cho d
21n + 5 chia hết cho d => 2(21n + 5) chia hết cho d
=>2(21n + 5) - 3(14n + 3) chia hết cho d
=> (42n + 10) - (42n + 9) chia hết cho d
=> d = ±1
=> \(\frac{14n+3}{21n+5}\) là phân số tối giản
Các bạn xem mình làm có đúng không ??
Đặt d = ƯCLN ( 14n + 3,21n + 5 ) ( d ∈ ℕ* )
Ta có : 14 n + 3 ⋮ d và 21n + 5 ⋮ d
⇒ 3( 14n + 3 ) ⋮ và 2( 21n + 5 ) ⋮ d ⇒ 42n + 9 ⋮ d và 42n + 10 ⋮ d
⇒ (42n + 10) - (42n + 9) ⋮ d ⇒ 1 ⋮ d . Do đó : d = 1
Vậy phân số trên là phân số tối giản