Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài này hay đấy
Áp dụng BĐT Cô-si cho 3 số không âm, ta có :
\(\frac{1+\sqrt{a}}{1+\sqrt{b}}+\frac{1+\sqrt{b}}{1+\sqrt{c}}+\frac{1+\sqrt{c}}{1+\sqrt{a}}\ge3\sqrt[3]{\frac{1+\sqrt{a}}{1+\sqrt{b}}.\frac{1+\sqrt{b}}{1+\sqrt{c}}.\frac{1+\sqrt{c}}{1+\sqrt{a}}}=3\)
Chứng minh \(\frac{1+\sqrt{a}}{1+\sqrt{b}}+\frac{1+\sqrt{b}}{1+\sqrt{c}}+\frac{1+\sqrt{c}}{1+\sqrt{a}}\le3+a+b+c\)( 1 )
đặt \(\sqrt{a}=x;\sqrt{b}=y;\sqrt{c}=z\)( x,y,z \(\ge\)0 )
do a,b,c là số nguyên
Nếu a = b = c = 0 thì x = y = z = 0 nên ( 1 ) đúng
Nếu a,b,c không đồng thời bằng 0 \(\Rightarrow\)x+ y + z \(\ge\)1
Ta có : VT ( 1 )
\(\Leftrightarrow\frac{\left(1+x\right)\left(1+y\right)-\left(1+x\right)y}{1+y}+\frac{\left(1+y\right)\left(1+z\right)-\left(1+y\right)z}{1+z}+\frac{\left(1+z\right)\left(1+x\right)-\left(1+z\right)x}{1+z}\)
\(=3+x+y+z-\left[\frac{\left(1+x\right)y}{1+y}+\frac{\left(1+y\right)z}{1+z}+\frac{\left(1+z\right)x}{1+x}\right]\)
\(\le3+x+y+z-\frac{\left(1+x\right)y+\left(1+y\right)z+\left(1+z\right)x}{1+x+y+z}=3+x+y+z-\frac{x+y+z+xy+yz+xz}{1+x+y+z}\)
\(=3+\frac{x^2+y^2+z^2+xy+yz+xz}{1+x+y+z}\le3+x^2+y^2+z^2\)
Cần chứng minh : \(\frac{x^2+y^2+z^2+xy+yz+xz}{1+x+y+z}\le x^2+y^2+z^2\)
\(\Leftrightarrow\left(x+y+z\right)\left(x^2+y^2+z^2\right)\ge xy+yz+xz\)
Mà \(\left(x+y+z\right)\left(x^2+y^2+z^2\right)\ge1.\left(x^2+y^2+z^2\right)\ge xy+yz+xz\)
suy ra đpcm

Ta có:
\(A=x-\left(\frac{1}{\sqrt{x}-\sqrt{x-1}}-\frac{1}{\sqrt{x}+\sqrt{x-1}}\right)\)
\(A=x-\frac{\sqrt{x}+\sqrt{x-1}-\sqrt{x}+\sqrt{x-1}}{\left(\sqrt{x}-\sqrt{x-1}\right)\left(\sqrt{x}+\sqrt{x-1}\right)}\)
\(A=x-\frac{2\sqrt{x-1}}{x-x+1}\)
\(A=x-2\sqrt{x-1}\)
\(A=\left(x-1\right)-2\sqrt{x-1}+1\)
\(A=\left(\sqrt{x-1}-1\right)^2\ge0\left(\forall x\ge1\right)\)
=> đpcm

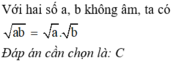

Khi \(a\ge0\) và \(a< 1\)
tick nha