Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ko chắc sẽ đúng
a)* Trên mp ABCD kéo dài MN và AB sao cho MN cắt AB = { I }
Xét mp (SMN) và (SAB) có:
S là điểm chung (1)
I là điểm chung (2)
=> (SMN) n (SAB) = { SI }
* Vì I thuộc mp ABCD (cmt)
G là trọng tâm tam giác SAB
Xét mp (GMN) và (SAB) có:
G và I là điểm chung
=> (GMN) n (SAB) = {GI}

Thưa chị, em không vẽ hình vì sợ duyệt, với lại em lớp 9 nên chỉ làm bài này dựa vào chút kiến thức lớp 8 thôi ạ.
a) Hình bình hành ABCD có O là tâm nên O là trung điểm của đường chéo BD.
Xét \(\Delta BDS\)có I và O lần lượt là trung điểm của BS, BD
\(\Rightarrow\)IO là đường trung bình của \(\Delta BDS\)\(\Rightarrow\)IO//DS
Mà \(DS\in mp\left(SAD\right)\)nên IO//\(mp\left(SAD\right)\)(đpcm)
Em không làm được câu b ạ, em xin lỗi chị.

a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
c: (SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=căn 3
=>góc SCA=60 độ

Trong mp(SAD) kẻ DF//SA
SA⊥AD => DF⊥AD mà AD⊥DC => AD⊥(DCF)
Kẻ CH⊥DF => CH⊥AD => CH⊥(SAD)
=> H là hình chiếu của C lên (SAD)
=> \(\widehat{\left(SC,\left(SAD\right)\right)}=\widehat{\left(SC,SH\right)}=\widehat{CSH}\)
ΔCFD=ΔSAB => ΔCFD đều cạnh a => CH= \(\dfrac{\sqrt{3}}{2}a\)
SC= \(\sqrt{2}a\)
Xét tam giác SCH vuông ở H ta có:
sin CSH= \(\dfrac{HC}{SC}\)=\(\dfrac{\sqrt{6}}{4}\)
=> \(\widehat{CSH}\)= arcsin\(\dfrac{\sqrt{6}}{4}\)
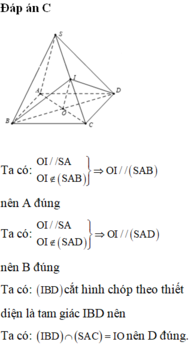



Chọn C.
+) Ta có:
+) Ta có:
+) Ta có: mp (IBD) cắt hình chóp theo thiết diện là tam giác IBD nên C sai.
+) Ta có: (IBD) ∩ (SAC) = IO nên D đúng.