Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
⇒ (SAD) ∩ (SBC) = Sx
Và Sx // AD // BC.
b) Ta có: MN // IA // CD
Mà
(G là trọng tâm của ∆SAB) nên
⇒ GN // SC
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒
Ta có:

Do IJ là đường thẳng trung bình của hình thang ABCD nên IJ // AB. Hai mặt phẳng (GIJ) và (SAB) lần lượt chứa hai đường thẳng song song nên giao tuyến của chúng là đường thẳng đi qua G và song song với AB. Đường thẳng này cắt SA tại điểm M và cắt SB tại N. vậy thiết diện là hình thang MIJN, với M, N là giao điểm của đường thẳng đi qua G và song song với AB với hai đường thẳng SA, SB.
Đáp án B.

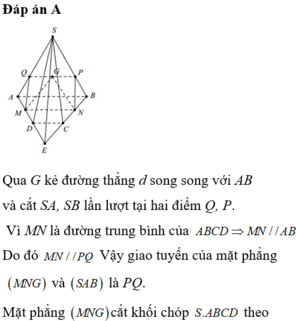
Kéo dài AB và CD cắt nhau tại E
\(\Rightarrow SE=\left(SAB\right)\cap\left(SCD\right)\)
Qua M kẻ đường thẳng d song song CD lần lượt cắt AC và AD tại F và G
Trong mp (SAC), qua F kẻ đường thẳng song song SA cắt SC tại P
Trong mp (SAD), qua G kẻ đường thẳng song song SA cắt SD tại Q
\(\Rightarrow\) Hình thang MPQG là thiết diện của (P) và chóp



Ko chắc sẽ đúng
a)* Trên mp ABCD kéo dài MN và AB sao cho MN cắt AB = { I }
Xét mp (SMN) và (SAB) có:
S là điểm chung (1)
I là điểm chung (2)
=> (SMN) n (SAB) = { SI }
* Vì I thuộc mp ABCD (cmt)
G là trọng tâm tam giác SAB
Xét mp (GMN) và (SAB) có:
G và I là điểm chung
=> (GMN) n (SAB) = {GI}
MN và AB // mà sao cắt nhau đc ạ