Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

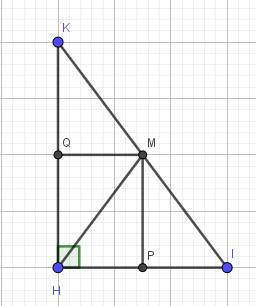
a) Do MP // HK (gt)
\(HK\perp HI\) (\(\Delta HIK\) vuông tại H)
\(\Rightarrow MP\perp HI\)
\(\Rightarrow\widehat{MPH}=90^0\)
Do MQ // HI (gt)
\(HI\perp HK\left(cmt\right)\)
\(\Rightarrow MQ\perp HK\)
\(\Rightarrow\widehat{MQH}=90^0\)
Tứ giác HQMP có:
\(\widehat{MQH}=\widehat{MPH}=\widehat{PAQ}=90^0\)
\(\Rightarrow HQMP\) là hình chữ nhật
b) \(\Delta MPH\) vuông tại P
\(\Rightarrow HM^2=PM^2+PH^2\left(Pytago\right)\)
\(\Rightarrow PM^2=HM^2-PH^2=10^2-6^2=64\)
\(\Rightarrow PM=8\left(cm\right)\)
Diện tích HQMP:
\(S_{HQMP}=PM.PH=8.6=48\left(cm^2\right)\)

a: Xét tứ giác HGEN có
HG//EN
HN//GE
Do đó: HGEN là hình bình hành
mà HE là tia phân giác
nên HGEN là hình thoi

a: Xét ΔHIK và ΔHNM có
HI/HN=HK/HM=5/2
góc H chung
=>ΔHIK đồng dạng với ΔHNM
b:
ΔHIK đồng dạng với ΔHNM
=>IK/NM=5/2
=>10/NM=5/2
=>NM=4cm
c: Xét ΔHIK và ΔHAI có
góc HIK=góc HAI(=góc HNM)
góc Hchung
=>ΔHIK đồng dạng với ΔHAI

a: Xét tứ giác AIHK có
\(\widehat{AIH}=\widehat{AKH}=\widehat{KAI}=90^0\)
=>AIHK là hình chữ nhật
b: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=12^2+16^2=400\)
=>BC=20(cm)
ΔABC vuông tại A có AM là đường trung tuyến
nên \(AM=\dfrac{1}{2}BC=\dfrac{1}{2}\cdot20=10\left(cm\right)\)
c: Xét ΔBHD có
BI là đường cao
BI là đường trung tuyến
Do đó: ΔBHD cân tại B
=>BH=BD
Xét ΔCEH có
CK là đường cao
CK là đường trung tuyến
Do đó: ΔCEH cân tại C
=>CH=CE
BC=BH+CH
mà BH=BD và CH=CE
nên BC=BD+CE
a. Tứ giác AIHK là hình vuông.
Vì tam giác ABC vuông tại A, nên đường cao AH cũng là đường trung tuyến của tam giác ABC. Do đó, AH cắt BC thành hai đoạn bằng nhau, tức là BH = CH.
Vì DI = IH và EK = KH, nên ta có DI = IH = EK = KH.
Do đó, AI = AH + IH = AH + DI = AH + EK = AK.
Vậy tứ giác AIHK là hình vuông.
b. Kẻ trung tuyến AM biết AB = 12 cm, AC = 16 cm. Ta cần tính AM.
Trung tuyến AM chia đôi đoạn BC, nên BM = MC.
Áp dụng định lý Pythagoras trong tam giác vuông ABC, ta có:
AB^2 + AC^2 = BC^2
12^2 + 16^2 = BC^2
144 + 256 = BC^2
400 = BC^2
BC = √400
BC = 20 cm
Vì BM = MC, nên BM = MC = BC/2 = 20/2 = 10 cm.
Vậy AM = AB + BM = 12 + 10 = 22 cm.
c. BC = BD + CE
Vì DI = IH và EK = KH, nên BD = DI và CE = EK.
Do đó, BC = BD + CE = DI + EK = DI + KH = DI + IH = DI + DI = 2DI.
Vậy DI = BC/2.

Bn tự vẽ hình nha![]()
a, Xét tứ giác HMKA có
góc MHA= 90 độ( mh ⊥ AB-gt)
góc MKA = 90 độ( MK⊥ AC - gt)
góc HAK = 90 độ( tam giác ABC ⊥ A-gt)
-> HMKA là hình chữ nhật ( tứ giác có 3 góc vuông)
-> HM song song AK; Hk=MA; HA=MK
ta có
HM song song ak(cmt)
M là trung điểm BC(gt)
-> H là trung điểm BA
-> Bh=HA=1/2 BA
mà HA=MK(cmt)
->BH=MK(1)
Xét tam giác ABC vuông tại A có
AM là đg trung tuyến(gt)
-> AM=MB=MC
mà MA=HK(cmt)
-> HK=BM(2)
Từ (1) và (2)
-> BMKH là hình bình hành( các cạnh đối bằng nhau là hình bình hành)
Sorry nhe mình ko bít lm câu C
Nếu hai câu trên đúng like cho mình nha >_<
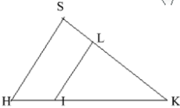
Ta có:
+ SL/LK = HI/IK → SH//LI
+ SL/SK = HI/HK → SH//LI
Chọn đáp án B.