Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

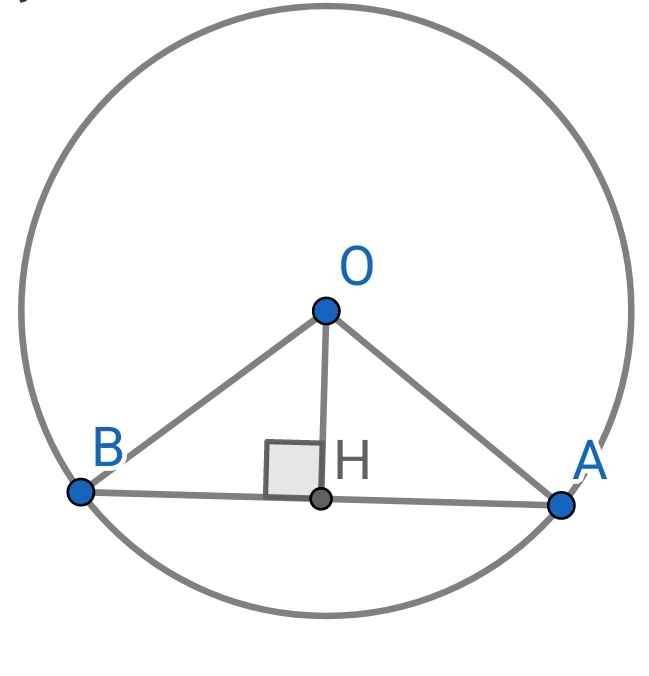
∆OBH vuông tại H
⇒ OB² = OH² + BH² (Pytago)
⇒ BH² = OB² - OH²
= 13² - 5²
= 144
⇒ BH = 12 (cm)
⇒ AB = 2BH = 2.12 = 24 (cm)
Chọn C

a: ΔOBC cân tại O
mà OH là đường cao
nên H là trung điểm của BC
=>HB=HC=12cm
=>\(OH=\sqrt{15^2-12^2}=9\left(cm\right)\)
b: Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
=>A nằm trên trung trực của BC
mà OH là trung trực của BC
nên O,H,A thẳng hàng
c: OA=OB^2/OH=15^2/9=25cm
=>AB=AC=20cm

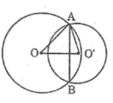
Gọi H là giao điểm của AB và OO’.
Vì OO’ là đường trung trực của AB nên:
OO’ ⊥ AB tại H
Suy ra: HA = HB = (1/2).AB = (1/2).24 = 12 (cm)
Áp dụng định lí Pitago vào tam giác vuông AOH, ta có:
A O 2 = O H 2 + A H 2
Suy ra: O H 2 = O A 2 - A H 2 = 15 2 - 12 2 = 81
OH = 9 (cm)
Áp dụng định lí pitago vào tam giác vuông AO’H, ta có:
A O ' 2 = O H ' 2 + A H 2
Suy ra: O ' H 2 = O ' A 2 - A H 2 = 13 2 - 12 2 = 25
O’H = 5 (cm)
Vậy OO’ = OH + O’H = 9 + 5 = 14 (cm)
Chọn B