Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

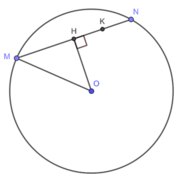
Ta có tam giác MON cân tại O
Mà ∠ OMN = 45 ° suy ra, tam giác OMN vuông cân tại O
OH là đường cao của tam giác MON
Suy ra, OH là đường trung tuyến của tam giác MON
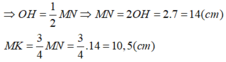
Đáp án: A

a: Xét ΔOAB vuông tại B có
\(OA^2=OB^2+AB^2\)
hay AB=8(cm)

Mình nói sơ qua nhá:
a) Ta có ΔABO là Δ vuông tại B
Ta tính được AB=8 nhờ vào định lí Py-ta-go
b) Do I là trung điểm của CD nên OI⊥CD, lại suy ra được OI⊥IA
Nên I sẽ chuyển động trên đường tròn đường kính OA (cố định) khi C thay đổi trên đường tròn
c) Chứng minh cho ΔABD∼ΔACB
Suy ra được AC.AD=AB2 không đổi
tk nha bạn
thank you bạn
(^_^)

a: ΔOAB cân tại O
mà OI là đường trung tuyến
nên OI là đường cao và OI là phân giác của \(\widehat{AOB}\)
Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
=>\(\widehat{OBC}=\widehat{OAC}=90^0\)
=>CB là tiếp tuyến của (O)
b: I là trung điểm của AB
=>IA=IB=AB/2=12cm
ΔOIA vuông tại I
=>\(OI^2+IA^2=OA^2\)
=>\(OI^2+12^2=13^2\)
=>\(OI^2=169-144=25\)
=>\(OI=\sqrt{25}=5\left(cm\right)\)
Xét ΔOAC vuông tại A có AI là đường cao
nên \(OI\cdot OC=OA^2\)
=>\(OC\cdot5=13^2=169\)
=>OC=33,8(cm)
Chọn C
C