Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mừng quá. Xong hết rồi. Hơn nửa tiếng bây giờ cũng được đền đáp =))
a) MB = MC (=MA) (giao điểm 2 tiếp tuyến cách đều tiếp điểm)
b) MA = MB = MC => T/g ABC vuông tại A => ^A = 90
T/g OAB cân tại O, có OM là đ/phân giác nên OM cũng là đ cao hay ^ANM = 90
Tương tự, ^APM = 90
=> đpcm
c) MO'/MO = O'C/BM (CMO' ~ BOM) = O'C/CM = CP/MP (CMO' ~ PMC) = MN/MP (PMC = NBM góc vuông - cạnh huyền - góc nhọn so le trong)
=> đpcm
d) Trong t/g vuông OMO' có MA là đường cao, OM^2 = OA.OO' <=> OM = 20 => BM = 12 (Pytago) => BC = 24
e) Dùng ta lét tìm ra OE, EC, còn OC tìm theo pytago trong t/g vuông OBC
f) ABKC là hình chữ nhật => AK cắt BC tại trung điểm M => đpcm

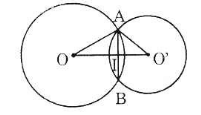
- Trường hợp 1: O và O' nằm khác phía đối với AB
Gọi I là giao điểm của OO' và AB. Theo tính chất đường nối tâm ta có
\(AB\perp OO'\) ; AI = IB = 12
Áp dụng định lí Pitago , ta được :
\(OI=\sqrt{OA^2-AI^2}=\sqrt{20^2-12^2}=\sqrt{256}=16\left(cm\right)\)
\(IO'=\sqrt{O'A^2-AI^2}=\sqrt{15^2-12^2}=\sqrt{81}=9\left(cm\right)\)
Vậy OO' = OI + IO' = 16 + 9 = 25 ( cm )
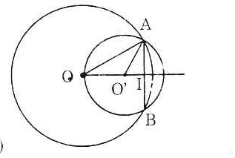
- Trường hợp 2: O và O' nằm cùng phía đối với AB
Như TH1 , ta lại có :
\(OI=\sqrt{OA^2-AI^2}=16\left(cm\right)\)
\(O'I=\sqrt{O'A^2-AI^2}=9\left(cm\right)\)
Vậy OO' = OI – O'I = 16 – 9 = 7 ( cm )

Từ một điểm A nằm bên ngoài đường tròn ( O ), kẻ các tiếp tuyến AB, AC với đường tròn ( B,C là các tiếp điểm )
a) Chứng minh rằng ABOC là tứ giác nội tiếp
b)Cho bán kính đường tròn ( O ) bằng 3cm, độ dài đoạn thẳng OA bằng 5cm. Tính độ dài đoạn thẳng BC
c) Gọi ( K ) là đường tròn qua A và tiếp xúc với đường thẳng BC tạo C. Đường trknf (K) và đường tròn (O ) cắt nhau tại điểm thứ hai là M. Chứng minh rằng đường thẳng BM đi qua trung điểm của đoạn thẳng AC

a) Trường hợp O và O’ nằm khác phía đối với AB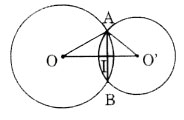
Ta có: AI =1/2 AB = 12
OI2 = OA2 – AI2
=400-144 =256
⇒ OI =16
O’I2 = O’A2 – AI2 =255 -144 =81
⇒ O’I = 9
Ta có: OO’ = OI + OI’ = 16 + 9 =25 (cm).
b) Trường hợp O và O’ nằm cùng phía đối với AB.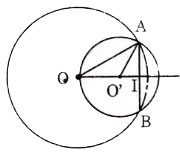
Ta có: OI2 = OA2 – AI2 = 256
⇒ OI =16
Tương tự O’I= 9
Do đó: OO’= OI – O’I =16 – 9= 7(cm)


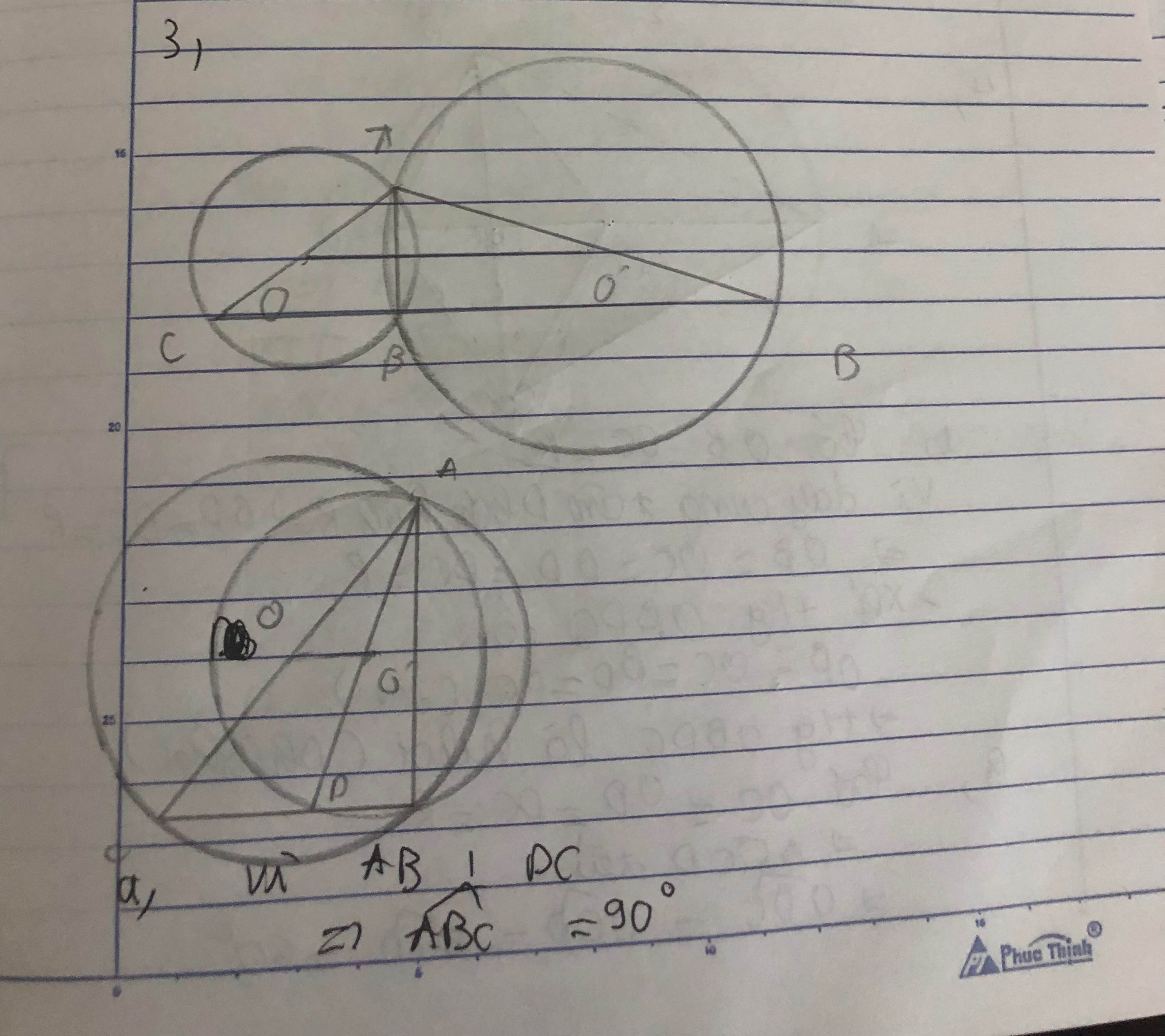
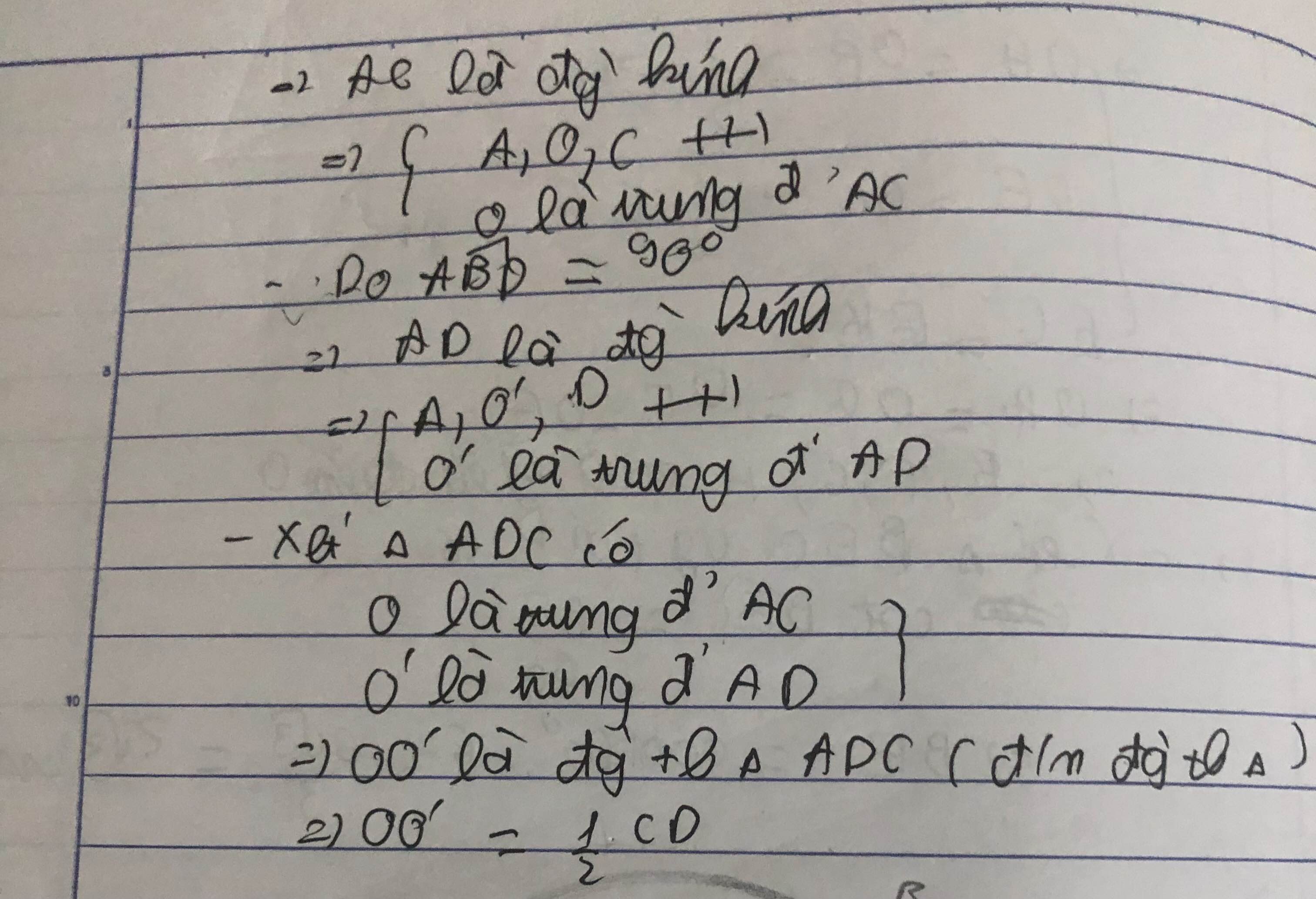
Gọi H là giao điểm của AB và OO’.
Vì OO’ là đường trung trực của AB nên:
OO’ ⊥ AB tại H
Suy ra: HA = HB = (1/2).AB = (1/2).24 = 12 (cm)
Áp dụng định lí Pitago vào tam giác vuông AOH, ta có:
A O 2 = O H 2 + A H 2
Suy ra: O H 2 = O A 2 - A H 2 = 15 2 - 12 2 = 81
OH = 9 (cm)
Áp dụng định lí pitago vào tam giác vuông AO’H, ta có:
A O ' 2 = O H ' 2 + A H 2
Suy ra: O ' H 2 = O ' A 2 - A H 2 = 13 2 - 12 2 = 25
O’H = 5 (cm)
Vậy OO’ = OH + O’H = 9 + 5 = 14 (cm)