Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

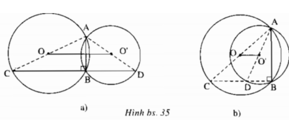
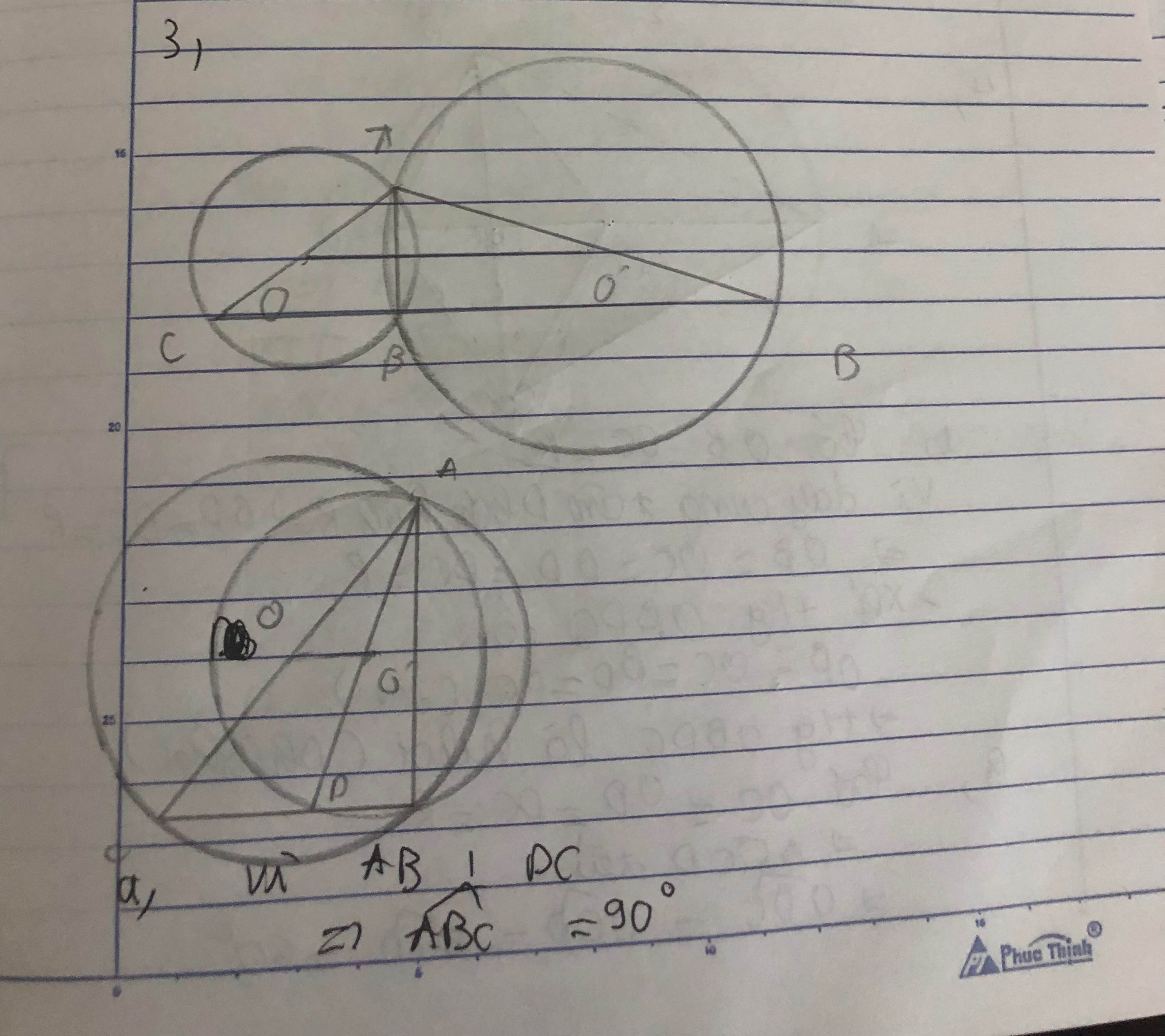
∠ (ABC) = 90 ° nên A, O, C thẳng hàng.
∠ (ABD) = 90 ° nên A, O’, D thẳng hàng.
OO’ là đường trung bình của tam giác ∆ ACD nên OO’ = 1/2CD.

 Kẻ OM ⊥ AD.
Kẻ OM ⊥ AD.
Theo tính chất đường kính vuông góc với một dây, ta có: MA = MC
Tương tự, kẻ O'N ⊥ AD => NA = ND.
Ta có:
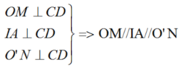
Vậy tứ giác OMNO' là hình thang vuông.
Ta còn có: IO = IO' (gt) và IA // OM
Do đó IA là đường trung bình của hình thang OMNO'.
=> AM = AN hay 2AM = 2AN
Hay AC = CD (đpcm)

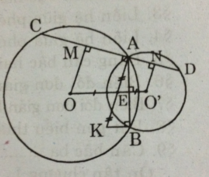
Ta có OO' là đường nối tâm của (O) và (O') nên OO' là đường trung trực của AB.
Suy ra IE ⊥ AB và EA = EB
Ta lại có IA = IK (do K là điểm đối xứng của A qua I).
Nên IE là đường trung bình của tam giác AKB.
Suy ra IE // KB
Mà IE ⊥ AB
Suy ra KB ⊥ AB (đpcm)

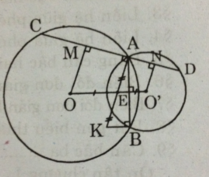
A B C O D E H I F
a) Xét \(\Delta ABE\)và \(\Delta ABD\)có :
\(\widehat{BAE}=\widehat{BAD}\); \(\widehat{ABE}=\widehat{BDE}\)
\(\Rightarrow\Delta ABE\approx\Delta ADB\left(g.g\right)\)
\(\Rightarrow\frac{AB}{AE}=\frac{AD}{AB}\Rightarrow AD.AE=AB^2\)( 1 )
Xét \(\Delta ABO\)vuông tại B ( do AB là tiếp tuyến ), đường cao BH ( tự c/m ), ta có hệ thức lượng
\(AH.AO=AB^2\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(AD.AE=AH.AO=AB^2\)
b) \(AD.AE=AH.AO\Rightarrow\frac{AE}{AH}=\frac{AO}{AD}\)
Xét \(\Delta AEH\)và \(\Delta AOD\)có :
\(\frac{AE}{AH}=\frac{AO}{AD}\); \(\widehat{EAH}\)( chung )
\(\Rightarrow\Delta AEH\approx\Delta AOD\left(c.g.c\right)\)\(\Rightarrow\widehat{AHE}=\widehat{ADO}\)( 3 )
Mà \(\Delta ODE\)cân tại O ( do OE = OD ) \(\Rightarrow\widehat{OED}=\widehat{ODE}\)( 4 )
Từ ( 3 ) và ( 4 ) suy ra \(\widehat{AHE}=\widehat{OED}\)
c) đường thẳng qua B vuông góc với CD tại I
Xét hai tam giác vuông BID và CBI có :
\(\widehat{IDB}=\widehat{CBI}\); \(\widehat{BID}=\widehat{BIC}=90^o\)
\(\Rightarrow\Delta BID\approx\Delta CIB\left(g.g\right)\) \(\Rightarrow\frac{ID}{IB}=\frac{IB}{IC}=\frac{DB}{BC}\)
\(\Rightarrow\frac{ID}{IB}.\frac{IB}{IC}=\frac{ID}{IC}=\frac{BD^2}{BC^2}\)
Mặt khác : \(\Delta DAC\)có : BI // AC
\(\Rightarrow\frac{FI}{AC}=\frac{DI}{DC}=\frac{DI}{DI+CI}=\frac{1}{1+\frac{CI}{DI}}=\frac{1}{1+\frac{BC^2}{BD^2}}=\frac{BD^2}{BD^2+BC^2}=\frac{BD^2}{4R^2}\)( R là bán kính )
\(\Rightarrow FI=\frac{BD^2.AC}{4R^2}\)( 5 )
Xét \(\Delta BCD\)và \(\Delta ACO\)có :
\(\widehat{BCD}=\widehat{OAC}\); \(\widehat{CBD}=\widehat{ACO}=90^o\)
\(\Rightarrow\Delta BCD\approx\Delta CAO\left(g.g\right)\)\(\Rightarrow\frac{BC}{AC}=\frac{BD}{OC}\Rightarrow BC=\frac{AC.BD}{R}\)( 6 )
Xét 2 tam giác vuông BIC và BCD có :
\(\widehat{BCD}\)( chung ) ; \(\widehat{BIC}=\widehat{CBD}=90^o\)
\(\Rightarrow\Delta BIC\approx\Delta DBC\)( g.g )
\(\Rightarrow\frac{IB}{BD}=\frac{BC}{CD}\Rightarrow IB=\frac{BC.BD}{2R}\)( 7 )
Từ ( 6 ) và ( 7 ) suy ra : \(IB=\frac{AC.BD^2}{2R^2}\)( 8 )
Từ ( 5 ) và ( 8 ) suy ra : \(IF=\frac{IB}{2}\Rightarrow\)F là trung điểm của IB
\(\Rightarrow HF\)là đường trung bình của \(\Delta BCI\)\(\Rightarrow HF//CD\)

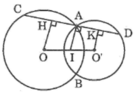
Kẻ OH ⊥ CD, O’K ⊥ CD
Ta có: IA ⊥ CD
Suy ra : OH // IA // O’K
Theo giả thiết : IO = IO’
Suy ra : AH = AK (tính chất đường thẳng song song cách đều) (1)
Ta có : OH ⊥ AC
Suy ra : HA = HC = (1/2).AC (đường kính dây cung) ⇒ AC = 2AH (2)
Lại có : O’K ⊥ AD
Suy ra : KA = KD = (1/2).AD (đường kính dây cung) ⇒ AD = 2AK (3)
Từ (1), (2) và (3) suy ra: AC = AD

mình mới học lớp 7 nhưng chỉ biết câu a sai thì thôi nhé ac=ad vì cái kia = cái này mà cái này = cái kia bạn chỉ cần nói với cô như vậy.Thôi nha
a/ Gọi E, F lần lược là trung điểm của AD, AC
\(\Rightarrow AI\)là đường trung bình của hình thang \(OFEO'\)
\(\Rightarrow AE=AF\)
\(\Rightarrow AD=AC\)
b/ Gọi G là giao điểm của AB với OO'
\(\Rightarrow IG\)là đường trung bình của \(\Delta ABK\)
\(\Rightarrow\)IG // BK
Mà \(IG⊥AB\)
\(\Rightarrow BK⊥AB\)
PS: Bạn vẽ hộ cái hình nhé