Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường tròn c: Đường tròn qua B_1 với tâm O Đường thẳng q: Tiếp tuyến của c qua A Đường thẳng q: Tiếp tuyến của c qua A Đoạn thẳng h: Đoạn thẳng [A, E] Đoạn thẳng i: Đoạn thẳng [B, E] Đoạn thẳng j: Đoạn thẳng [C, E] Đoạn thẳng k: Đoạn thẳng [O, C] Đoạn thẳng l: Đoạn thẳng [O, B] Đoạn thẳng m: Đoạn thẳng [A, B] Đoạn thẳng n: Đoạn thẳng [A, C] Đoạn thẳng p: Đoạn thẳng [B, D] Đoạn thẳng a: Đoạn thẳng [B, P] Đoạn thẳng b: Đoạn thẳng [C, Q] Đoạn thẳng d: Đoạn thẳng [P, Q] Đoạn thẳng g_1: Đoạn thẳng [B, C] Đoạn thẳng i_1: Đoạn thẳng [M, A] Đoạn thẳng k_1: Đoạn thẳng [O, M] O = (-0.28, -0.29) O = (-0.28, -0.29) O = (-0.28, -0.29) Điểm B: Điểm trên c Điểm B: Điểm trên c Điểm B: Điểm trên c Điểm C: Điểm trên c Điểm C: Điểm trên c Điểm C: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm E: Giao điểm của f, g Điểm E: Giao điểm của f, g Điểm E: Giao điểm của f, g Điểm D: Giao điểm của c, h Điểm D: Giao điểm của c, h Điểm D: Giao điểm của c, h Điểm P: Giao điểm của r, s Điểm P: Giao điểm của r, s Điểm P: Giao điểm của r, s Điểm Q: Giao điểm của r, t Điểm Q: Giao điểm của r, t Điểm Q: Giao điểm của r, t Điểm M: Trung điểm của g_1 Điểm M: Trung điểm của g_1 Điểm M: Trung điểm của g_1 Điểm F: Giao điểm của e, d Điểm F: Giao điểm của e, d Điểm F: Giao điểm của e, d
a. Ta thấy ngay tứ giác OBEC có hai góc vuông đối nhau nên nó là tứ giác nội tiếp.
b. Câu này cô thấy cần sửa đề thành AB.AP = AD.AE mới đúng.
Gọi Aq là tiếp tuyến tại A của đường tròn (O). Khi đó ta có: \(\widehat{APE}=\widehat{BAq}\) (so le trong)
Mà \(\widehat{BAq}=\widehat{BDA}\) (Cùng chắn cung BA) nên \(\widehat{APE}=\widehat{BDA}\)
Vậy thì \(\Delta ABD\sim\Delta AEP\left(g-g\right)\Rightarrow\frac{AB}{AE}=\frac{AD}{AP}\Rightarrow AB.AP=AE.AD\)
c. +) Ta thấy \(\Delta BDE\sim\Delta ABE\left(g-g\right)\Rightarrow\frac{BD}{AB}=\frac{BE}{AE}\)
Tương tự \(\Delta CDE\sim\Delta ACE\left(g-g\right)\Rightarrow\frac{CD}{AC}=\frac{DE}{AE}\)
Mà BE = CE nên \(\frac{BD}{AB}=\frac{CD}{AC}\)
Lại có \(\Delta ABD\sim\Delta AEP\left(g-g\right)\Rightarrow\frac{BD}{EP}=\frac{AB}{AE}\Rightarrow EP=\frac{BD.AE}{AB}\)
Tương tự \(\Delta ACD\sim\Delta AEQ\left(g-g\right)\Rightarrow\frac{AC}{AE}=\frac{CD}{EQ}\Rightarrow EQ=\frac{CD.AE}{AC}=\frac{BD.AE}{AB}=EP\)
Vậy EP = EQ.
+) Ta thấy ngay \(\Delta ABC\sim\Delta AQP\Rightarrow\frac{BC}{QP}=\frac{AC}{AP}\Rightarrow\frac{BC:2}{QP:2}=\frac{AC}{QP}\)
\(\Rightarrow\frac{MC}{PE}=\frac{AC}{AP}\)
Lại có \(\widehat{ACM}=\widehat{APE}\) (Cùng bằng \(\widehat{BDA}\))
Từ đó suy ra \(\Delta AMC\sim\Delta AEP\Rightarrow\widehat{MAC}=\widehat{PAE}\)
d. Ta có BD.AC = AB.CD
Lại có do ABCD là tứ giác nội tiếp nên
AD.BC = AB.CD + AC.BD = 2AB.CD (Định lý Ptoleme) \(\Rightarrow2MC.AD=2AB.CD\Rightarrow MC.AD=AB.CD\)
\(\Rightarrow\frac{MC}{AB}=\frac{CD}{AD}\)
Lại thấy \(\widehat{BAD}=\widehat{BCD}\Rightarrow\Delta BAD\sim\Delta MCD\left(c-g-c\right)\)
Mà \(\Delta BAD\sim\Delta MAC\Rightarrow\Delta MCD\sim\Delta MAC\)
\(\Rightarrow\frac{MC}{MA}=\frac{MD}{MC}\Rightarrow MA.MD=MC^2=\frac{BC^2}{4}.\)

Đường tròn c: Đường tròn qua B với tâm O Đoạn thẳng h: Đoạn thẳng [A, B] Đoạn thẳng i: Đoạn thẳng [B, C] Đoạn thẳng j: Đoạn thẳng [A, C] Đoạn thẳng n: Đoạn thẳng [O, C] Đoạn thẳng p: Đoạn thẳng [F, C] Đoạn thẳng q: Đoạn thẳng [C, H] Đoạn thẳng r: Đoạn thẳng [B, E] Đoạn thẳng s: Đoạn thẳng [C, E] Đoạn thẳng t: Đoạn thẳng [A, F] O = (1.42, 2.28) O = (1.42, 2.28) O = (1.42, 2.28) B = (5.54, 2.28) B = (5.54, 2.28) B = (5.54, 2.28) Điểm A: Giao điểm đường của c, f Điểm A: Giao điểm đường của c, f Điểm A: Giao điểm đường của c, f Điểm C: Điểm trên c Điểm C: Điểm trên c Điểm C: Điểm trên c Điểm H: Giao điểm đường của k, h Điểm H: Giao điểm đường của k, h Điểm H: Giao điểm đường của k, h Điểm M: Trung điểm của A, C Điểm M: Trung điểm của A, C Điểm M: Trung điểm của A, C Điểm N: Trung điểm của H, C Điểm N: Trung điểm của H, C Điểm N: Trung điểm của H, C Điểm F: Giao điểm đường của g, m Điểm F: Giao điểm đường của g, m Điểm F: Giao điểm đường của g, m Điểm E: Giao điểm đường của g, l Điểm E: Giao điểm đường của g, l Điểm E: Giao điểm đường của g, l
a) Ta thấy \(\widehat{ACB}\) là góc nội tiếp chắn nửa đường tròn AB. Vậy nên \(\widehat{ACB}=\frac{sđ\widebat{AB}}{2}=\frac{180^o}{2}=90^o\)
Vậy tam giác ABC là tam giác vuông tại C.
b) Do M là trung điểm của dây cung AC. Theo tính chất đường kính, dây cung, ta có \(OM\perp AC\)
Xét tứ giác OMCH có \(\widehat{OMC}=\widehat{OHC}=90^o\) nên OMCH là tứ giác nội tiếp.
Đường tròn ngoại tiếp tứ giác trên có đường kinh là OC nên tâm I của đường tròn là trung điểm OC.
c) Xét tam giác vuông ABE có đường cao BC. Áp dụng hệ thức lượng trong tam giác ta có:
\(EC.EA=BE^2\)
Xét tam giác vuông BCE, theo định lý Pi-ta-go, ta có:
\(BE^2=OE^2-OB^2=OE^2-R^2\)
Vậy ta có ngay \(EC.EA=OE^2-R^2\)
d) Ta thấy CH // BE nên áp dụng định lý Talet ta có:
\(\frac{NH}{BF}=\frac{NC}{FE}\left(=\frac{AH}{AB}\right)\)
Lại có NH = HC nên BF = FE
Xét tam giác vuông BCE có CF là trung tuyến ứng vớ cạnh huyền nên FC = FB.
Vậy thì \(\Delta OCF=\Delta OBF\left(c-c-c\right)\Rightarrow\widehat{OCF}=\widehat{OBF}=90^o\)
hay CF là tiếp tuyến của đường tròn (I)

a) AM là đường phân giác \(\widehat{BAC}\)
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\)\(\Rightarrow\widebat{BM}=\widebat{CM}\)
=> M là điểm chính giữa cung BC
=> OM _|_ BC (đpcm)
b) AN là phân giác \(\widehat{CAt}\)
=> \(\widehat{tAN}=\widehat{NAC}\)mà \(\widehat{tAN}=\widehat{NCB}\)(Tứ giác ANCB nội tiếp)
và \(\widehat{NAC}=\widehat{NMC}\)(tứ gics ANCB nội tiếp)
=> \(\widehat{NCB}=\widehat{NMC}\)
Xét tam giác NCD và tam giác NMC có:
\(\widehat{MNC}\)chung
\(\widehat{NCB}=\widehat{NMC}\left(cmt\right)\)
=> Tam giác NCD đồng dạng với tam giác NMC (g.g)
=> \(\widehat{NCM}=\widehat{NDC}\)mà \(\widehat{NDC}=90^o\)và \(\widehat{NCM}=90^o\)
=> NC _|_ CM
Xét tam giác NCM nội tiếp có NC _|_ CM
=> NM là đường kính
=> N,O,M thẳng hàng
c) Tam giác MAN nội tiếp đường kín MN
=> AM _|_ AN => Tam giác KAD vuông tại A
Xét tam giác KAD vuông tại A có AI là đường trung bình
=> AI=ID
=> Tam giác AID cân tại A
=> \(\widehat{IAD}=\widehat{IDA}\)(tính chất tam giác cân) hay \(\widehat{IAB}+\widehat{BAD}=\widehat{IDA}\)
Lại có \(\widehat{DAC}+\widehat{DCA}=\widehat{IDA}\)(tính chất góc ngoài)
\(\Rightarrow\widehat{IAB}+\widehat{BAD}=\widehat{DAC}+\widehat{DCA}\)
mà \(\widehat{BAD}=\widehat{DAC}\)(AD là phân giác) => \(\widehat{IAB}=\widehat{DCA}\)
mà 2 góc này nằm ở vị trí góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung
=> IA là tiếp tuyến của (O)

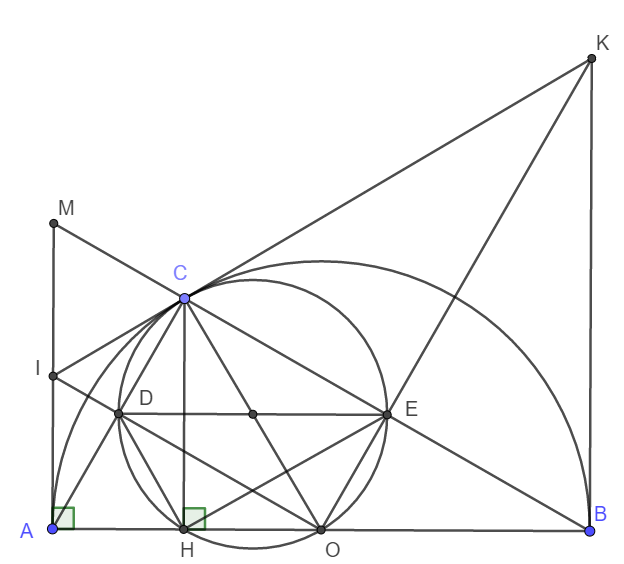
a) Do C thuộc nửa đường tròn nên \(\widehat{ACB}=90^o\) hay AC vuông góc MB.
Xét tam giác vuông AMB có đường cao AC nên áp dụng hệ thức lượng ta có:
\(BC.BM=AB^2=4R^2\)
b) Xét tam giác MAC vuông tại C có CI là trung tuyến ứng với cạnh huyền nên IM = IC = IA
Vậy thì \(\Delta ICO=\Delta IAO\left(c-c-c\right)\)
\(\Rightarrow\widehat{ICO}=\widehat{IAO}=90^o\)
Hay IC là tiếp tuyến tại C của nửa đường tròn.
c) Xét tam giác vuông AMB có đường cao AC, áp dụng hệ thức lượng ta có:
\(MB.MC=MA^2=4IC^2\Rightarrow IC^2=\frac{1}{4}MB.MC\)
Xét tam giác AMB có I là trung điểm AM, O là trung điểm AB nên IO là đường trung bình tam giác ABM.
Vậy thì \(MB=2OI\Rightarrow MB^2=4OI^2\) (1)
Xét tam giác vuông MAB, theo Pi-ta-go ta có:
\(MB^2=MA^2+AB^2=MA^2+4R^2\) (2)
Từ (1) và (2) suy ra \(4OI^2=MA^2+4R^2.\)
d) Do IA, IC là các tiếp tuyến cắt nhau nên ta có ngay \(AC\perp IO\Rightarrow\widehat{CDO}=90^o\)
Tương tự \(\widehat{CEO}=90^o\)
Xét tứ giác CDOE có \(\widehat{CEO}=\widehat{CDO}=90^o\)mà đỉnh E và D đối nhau nên tứ giác CDOE nội tiếp đường tròn đường kính CO.
Xét tứ giác CDHO có: \(\widehat{CHO}=\widehat{CDO}=90^o\) mà đỉnh H và D kề nhau nên CDHO nội tiếp đường tròn đường kính CO.
Vậy nên C, D, H , O, E cùng thuộc đường tròn đường kính CO.
Nói cách khác, O luôn thuộc đường tròn ngoại tiếp tam giác HDE.
Vậy đường tròn ngoại tiếp tam giác HDE luôn đi qua điểm O cố định.

a gọi I là trung điểm của A=> I thuộc đường tròn (O) vì OI-1/2.)OA=1.2.2R=R= BK
có AB,AC là tiếp tuyến của (O)
=>góc ABO=góc ACO=90 độ
=> tam giác ABO vuông tại B, có BI là đường trung tuyến
=> BI=OI=IA
có OI=OC=OB
=> tứ giác OBIC là hình thoi
=> OI là đường phân giác của góc BIC(tính chất hình thoi) hay AI là phân giác góc BAC(1)
lại có ABOC nội tiếp(O) (cmt)
=> AO vuông góc với BC hay AI vuông góc với BC(2), AB=AC(3)
từ (1)(2)(3)=> tam giác ABC đều
O A B C D E
a) Ta thấy ngay \(\widehat{BDA}=\widehat{CBA}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cung cùng chắn một cung)
Vậy nên \(\Delta ABC\sim\Delta ADB\left(g-g\right)\)
b) Do \(\Delta ABC\sim\Delta ADB\Rightarrow\frac{AB}{AD}=\frac{AC}{AB}\Rightarrow AB^2=AD.AC\)
Xét tam giác vuông OBA có \(AB=\sqrt{AO^2-OB^2}=\sqrt{4R^2-R^2}=R\sqrt{3}\)
Vậy nên \(AD.AC=AB^2=3R^2\)
c) Ta thấy rằng \(\Delta ABC\sim\Delta ADB\Rightarrow\widehat{ABC}=\widehat{ADB}\)
Vậy thì \(\widehat{BEA}=\widehat{DBE}+\widehat{BDE}=\widehat{ABC}+\widehat{CBE}=\widehat{ABE}\)
Suy ra tam giác ABE cân tại A hay AB = AE.
Do A, B cố định nên AE không đổi.
Vậy khi cát tuyến ACD quay xung quanh A thì E di chuyển trên đường tròn tâm A, bán kính AB.
d) Ta có AC.AD = 3R2 ; AC + AD = 7R/2
nên ta có phương trình \(AC\left(\frac{7R}{2}-AC\right)=3R^2\)
\(\Leftrightarrow AC^2-\frac{7R}{2}AC+3R^2=0\Leftrightarrow AC=2R\)
\(\Rightarrow AD=\frac{3R}{2}\)
a: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó: ΔABC vuông tại A
Xét ΔABC vuông tại A có sin ACB=AB/BC=1/2
nen góc ACB=30 độ
=>góc ABC=60 độ
b: Ta có: ΔOAD cân tại O
mà OH là đường cao
nên OH là trung trực của AD và OH là phân giác của góc AOD
=>BC là trung trực của AD
Xét ΔCAD có
CH vừa là đường cao, vừa là trungtuyến
nên ΔCAD cân tại C
=>góc ACD=2*góc ACB=60 độ
=>ΔCAD đều
c: Xét ΔEAO và ΔEDO có
OA=OD
góc AOE=góc DOE
OE chung
Do đó; ΔEAO=ΔEDO
=>góc EAO=90 độ
=>EA là tiếp tuyến của (O)