Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

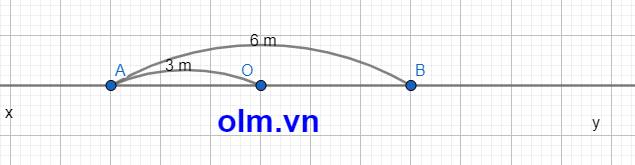
a, Các cặp tia đối nhau chung gốc A lần lượt là:
Ax và AO; Ax và AB; Ax và AY
b, Vì OA và OB là hai tia đối nhau nên O nằm giữa A và B
⇒ OA + OB = AB
⇒ OB = AB - OA
Độ dài đoạn OB là: 6 - 3 = 3 (cm)
c, Vì O nằm giữa A và B mà OA = OB = 3 cm nên O là trrung điểm AB

a: Các cặp tia đối nhau gốc A là:
AB,Ax
AO,Ax
Ay,Ax
b: Trên tia Ay, ta có: AO<AB(3cm<6cm)
nên O nằm giữa A và B
=>AO+OB=AB
=>OB+3=6
=>OB=3(cm)
c: Vì O nằm giữa A và B
và OA=OB(=3cm)
nên O là trung điểm của AB
a) Cặp tia đối nhau gốc A trên hình vẽ là tia OA và tia AO.
b) Độ dài đoạn thẳng OB có thể tính bằng cách sử dụng định lý Pythagoras trong tam giác vuông OAB:
OB² = OA² + AB²
OB² = 3² + 6²
OB² = 9 + 36
OB² = 45
OB = √45 ≈ 6.71 cm
c) Điểm O không phải là trung điểm của đoạn thẳng AB. Để chứng minh điều này, ta có thể tính độ dài của OA và OB:
OA = 3 cm
OB = 6.71 cm
Ta thấy OA ≠ OB, do đó O không là trung điểm của AB.
tick mik nha

a: Trên tia Ox, ta có: OM<ON
nên M nằm giữa O và N
=>OM+MN=ON
=>MN+4=8
=>MN=4(cm)
b: Ta có: M nằm giữa O và N
MN=MO(=4cm)
Do đó: M là trung điểm của ON
c: Trên tia Ox, ta có: OP<OM
nên P nằm giữa O và M
=>OP+PM=OM
=>PM+2=4
=>PM=2(cm)
Ta có: P nằm giữa O và M
mà OP=PM(=2cm)
nên P là trung điểm của OM
Trên tia Ox, ta có: OM<OQ
nên M nằm giữa O và Q
=>OM+MQ=OQ
=>MQ+4=6
=>MQ=2(cm)
Vì MP=MQ(=2cm)
nên M là trung điểm của PQ
Trên tia Ox, ta có: OQ<ON
nên Q nằm giữa O và N
=>OQ+QN=ON
=>QN+6=8
=>QN=2(cm)
Vì MQ=QN(=2cm)
nên Q là trung điểm của MN

a) Các đoạn thẳng có trong hình là:
\(BF,AE,AF,OF,OE,AB,EF,OB,OA,BE\)
b) Độ dài đoạn thằng EF là:
\(EF=AE+AF=2+6=8\left(cm\right)\)
c) Ta có:
\(AB+OA=OB\Rightarrow AB=OB-OA=8-4=4\left(cm\right)\)
Mà: \(AB=OA\)
⇒ A nằm chính giữa O và B hay A là trung điểm của OB
d) Ta có:
\(BE+AE=AB\Rightarrow BE=AB-AE=4-2=2\left(cm\right)\)
Mà: \(BE=AE\)
Vậy E nằm chính giữa A và B hay E là trung điểm của AB

Kí hiệu tam giác vt là t/g nhé
a) Xét t/g AOC và t/g BOD có:
OA = OB (gt)
CAO = DBO (gt)
AC = BD (gt)
Do đó, t/g AOC = t/g BOD (c.g.c)
=> OC = OD (2 cạnh tương ứng) (1)
Tương tự ta cũng có t/g AOE = t/g BOF (c.g.c)
=> OE = OF (2 cạnh tương ứng) (2)
(1) và (2) là đpcm
b) t/g AOC = t/g BOD (câu a)
=> AOC = BOD (2 góc tương ứng)
Mà AOC + COB = 180o ( kề bù)
nên BOD + COB = 180o
=> COD = 180o
=> C,O,D thẳng hàng
trường hợp c` lại tương tự
c) Có: AC = BD (gt); AE = BF (gt)
=> AE - AC = BF - BD ( vì hình của mk AE > AC c` nếu hình bn vẽ AC > AE thì ngược lại)
=> EC = FD
Vì BAx = ABy mà 2 góc này ở vị trí so le trong nên Ax // By
Xét t/g CEO và t/g DFO có:
CEO = DFO (so le trong)
EC = FD (cmt)
ECO = FDO (so le trong)
Do đó, t/g CEO = t/g DFO (g.c.g)
=> CO = DO (2 cạnh tương ứng)
EO = FO (2 cạnh tương ứng)
Từ đó dễ dàng suy ra t/g COF = t/g DOE (c.g.c)
=> CF = DE (2 cạnh tương ứng) (đpcm)
