Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét ΔABE=ΔACD
có: AB=AC
^A là góc chung
AD=AE
==> ΔABE=ΔACD(c-g-c)
b, Xét ΔKBD và ΔKCE
^K1=^K2 (đđ)
BD=CE( AB=AC và AD=AE)
KD=KE
==> ΔKBD=ΔKCE (c-g-c)
c, Xét ΔAKB và ΔAKC
có AK cạnh chung
KB=KC
AB=AC
=>ΔAKB = ΔAKC (c-c-c)
=> ^BAK= ^CAK mà AK là cạnh chung
=> AK là tia phân giác của góc BAC

a/ Xét tam giác BCD và tam giác BCE có
-góc B = góc C
-BD = EC
-BC: cạnh chung
=> tam giác BCD = tam giác BCE (cạnh góc cạnh)
=> BE=CD (2 cạnh tương ứng)
b/ Xét tam giác KBD và tam giác KCE có
-Góc BKD = góc CKE (đối đỉnh)
-BD=CE
-KB=KC
=> tam giác KBD = tam giác KCE

Ta có hình vẽ:
A B C D E K
a/ Xét \(\Delta ABE\) và \(\Delta ACD\) có:
AB = AC (gt)
\(\widehat{A}:chung\)
AE = AD (gt)
\(\Rightarrow\Delta ABE=\Delta ACD\left(c-g-c\right)\left(đpcm\right)\)
b/ Vì \(\Delta ABE=\Delta ACD\left(ýa\right)\)
\(\Rightarrow\left\{{}\begin{matrix}BE=CD\\\widehat{ABE}=\widehat{ACD}\end{matrix}\right.\) (đpcm)
c/ Ta có: AD + BD = AB
AE + CE = AC
mà AD = AE(gt) ; AB = AC(gt)
=> BD = CE
Xét \(\Delta DBC\) và \(\Delta ECB\) có:
BD = CE (cmt)
\(\widehat{DBC}=\widehat{ECB}\) (\(\Delta ABC\) cân tại A)
BC: chung
=> \(\Delta DBC=\Delta ECB\left(c-g-c\right)\)
=> \(\widehat{BDC}=\widehat{CEB}\) (g t/ứng)
Xét \(\Delta KBD\) và \(\Delta KCE\) có:
\(\widehat{ABE}=\widehat{ACD}\left(đãcm\right)\)
BD = CE (đã cm)
\(\widehat{BDC}=\widehat{CEB}\left(cmt\right)\)
=> \(\Delta KBD=\Delta KCE\left(g-c-g\right)\)
=> KB = KC (c t/ứng)
=> \(\Delta KBC\) là tam giác cân tại K
Tự vẽ hình nhoa!
a) Vì \(\Delta ABC\) cân tại A
\(\Rightarrow AB=AC\) và \(\widehat{ABC}=\widehat{ACB}\)
Xét \(\Delta ABE\) và \(\Delta ACD\) có:
\(AB=AC\)
\(\widehat{A}\) chung
\(AE=AD\left(gt\right)\)
\(\Rightarrow\Delta ABE=\Delta ACD\left(c.g.c\right)\)
b) Vì \(\Delta ABE=\Delta ACD\) (câu a)
\(\Rightarrow BE=CD\) và \(\widehat{ABE}=\widehat{ACD}\)
c) Ta có: \(\widehat{ABC}-\widehat{ABE}=\widehat{ACB}-\widehat{ACD}\)
\(\Rightarrow\widehat{EBC}=\widehat{DCB}\)
hay \(\widehat{KBC}=\widehat{KCB}\)
\(\Rightarrow\Delta KBC\) cân tại K.

tự vẽ hình
a) Xét tam giác ABE và tam giác ACD, ta có:
Góc BAE= góc DAC(hay góc A là góc chung)
AD=AC(gt)
AD=AE(gt)
Vậy tam giác ABE = tam giác ACD (c-g-c)
=> BE=CD ( cặp cạnh t/ứng)
=> góc ABE=góc ACD (cặp góc t/ứng) hay góc ABK=góc ACK
b) Vì AB=AC, AD=AE => BD=CE( vì AD+BD=AB;AE+EC=AC)
tam giác DBK có: góc D+góc B+góc K=180 độ
tam giác KCE có: góc K+góc C+góc E=180 độ
mà Góc B= góc C(cmt) và Góc K1=Góc K1(đối đỉnh)---bạn tự kí hiệu nha :")
=> góc D=góc E
Xét tam giác BKD và tam giác KCE, ta có:
Góc BDK=góc KEC(cmt)
Góc DBK=góc ECK(cmt)
DB=CE(cmt)
Vậy tam giác BKD = tam giác KCE(g-c-g)
=> DK=EK(cặp cạnh tướng ứng)
c) Xét tam giác ADK và tam giác AEK, ta có:
AD=AE(gt)
DK=KE(cmt)
AK là cạnh chung
Vậy tam giác ADK= tam giác AEK(c-c-c)
=> góc DAK=góc EAK(cặp góc t/ứng) hay góc BAK=góc CAK
=> AK là p/g của góc BAC
d) Góc BAK=góc CAK hay góc BAI=góc CAI
Xét tam giác BAI và tam giác CAI, ta có:
AB=AC(gt)
AI là cạnh chung
Góc BAI=góc CAI (cmt)
Vậy tam giác BAI = tam giác CAI(c-g-c)
=>Góc AIB=góc AIC(cặp góc t/ứng)
mà góc AIB+góc AIC=180 độ => AIB=AIC=90 độ
=> AI vuông góc với BC

A B C D E F
| GT | △ABC: AB < AC. BAD = DAC = BAC/2 (D E F |
| KL | a, △ABD = △AED b, AD ⊥ FC c, △BDF = △EDC ; BF = EC d, F, D, E thẳng hàng |
Bài làm:
a, Xét △ABD và △AED
Có: AB = AE (gt)
BAD = DAE (gt)
AD là cạnh chung
=> △ABD = △AED (c.g.c)
b, Vì △ABD = △AED (cmt)
=> BD = ED (2 cạnh tương ứng)
=> D thuộc đường trung trực của BE (1)
Vì AB = AE (gt) => A thuộc đường trung trực của BE (2)
Từ (1) và (2) => AD là đường trung trực của BE
=> AD ⊥ FC
c, Vì △ABD = △AED (cmt)
=> ABD = AED (2 góc tương ứng)
Ta có: ABD + DBF = 180o (2 góc kề bù)
AED + DEC = 180o (2 góc kề bù)
Mà ABD = AED (cmt)
=> DBF = DEC
Lại có: AB + BF = AF
AE + EC = AC
Mà AB = AE (gt) ; AF = AC (gt)
=> BF = EC
Xét △BDF và △EDC
Có: BD = ED (cmt)
DBF = DEC (cmt)
BF = EC (cmt)
=> △BDF = △EDC (c.g.c)
d, Vì △BDF = △EDC (cmt)
=> BDF = EDC (2 góc tương ứng)
Ta có: BDE + EDC = 180o (2 góc kề bù)
=> BDE + BDF = 180o
=> FDE = 180o
=> 3 điểm F, D, E thẳng hàng

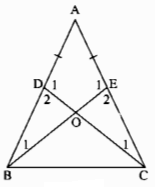
a) Xét ∆BEA và ∆CDA, ta có:
BA = CA (gt)
\(\widehat{A}\)chung
AE = AD (gt)
Suy ra: ∆BEA = ∆CDA (c.g.c)
Vậy BE = CD (hai cạnh tương ứng)
b) ∆BEA = ∆CDA (chứng minh trên)
⇒\(\widehat{\text{B1}}=\widehat{\text{C1}}\);\(\widehat{\text{E1}}=\widehat{\text{D1}}\) (hai góc tương ứng)
\(\widehat{\text{E1}}+\widehat{\text{E2}}\)=180o (hai góc kề bù)
\(\widehat{\text{D1}}+\widehat{\text{D2}}\)=180o (hai góc kề bù)
Suy ra: \(\widehat{\text{E2}}=\widehat{\text{D2}}\)
AB = AC (gt)
⇒ AE + EC = AD + DB mà AE = AD (gt) => EC = DB
Xét ∆ODB và ∆OCE, ta có:
\(\widehat{\text{E2}}=\widehat{\text{D2}}\) (chứng minh trên)
DB = EC (chứng minh trên)
\(\widehat{\text{B1}}=\widehat{\text{C1}}\)(chứng minh trên)
Suy ra: ∆ODB = ∆OEC (g.c.g)
 BC)
BC)
Hình bạn tự vẽ nha!
a) Xét 2 \(\Delta\) \(ABE\) và \(ACD\) có:
\(AE=AD\left(gt\right)\)
\(AB=AC\left(gt\right)\)
\(\widehat{A}\) chung
=> \(\Delta ABE=\Delta ACD\left(c-g-c\right).\)
b) Theo câu a) ta có \(\Delta ABE=\Delta ACD.\)
=> \(\widehat{AEB}=\widehat{ADC}\) (2 góc tương ứng).
=> \(\widehat{ABE}=\widehat{ACD}\) (2 góc tương ứng)
Hay \(\widehat{DBI}=\widehat{ECI}.\)
Ta có:
\(\left\{{}\begin{matrix}\widehat{ADC}+\widehat{BDC}=180^0\\\widehat{AEB}+\widehat{CEB}=180^0\end{matrix}\right.\) (các góc kề bù).
Mà \(\widehat{AEB}=\widehat{ADC}\left(cmt\right)\)
=> \(\widehat{BDC}=\widehat{CEB}.\)
Hay \(\widehat{BDI}=\widehat{CEI}.\)
Lại có:
\(\left\{{}\begin{matrix}AD+DB=AB\\AE+EC=AC\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\AD=AE\left(gt\right)\end{matrix}\right.\)
=> \(DB=EC.\)
Xét 2 \(\Delta\) \(IBD\) và \(ICE\) có:
\(\widehat{DBI}=\widehat{ECI}\left(cmt\right)\)
\(BD=EC\left(cmt\right)\)
\(\widehat{BDI}=\widehat{CEI}\left(cmt\right)\)
=> \(\Delta IBD=\Delta ICE\left(g-c-g\right)\left(đpcm\right).\)
Chúc bạn học tốt!