Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tự vẽ hình
a) Xét tam giác ABE và tam giác ACD, ta có:
Góc BAE= góc DAC(hay góc A là góc chung)
AD=AC(gt)
AD=AE(gt)
Vậy tam giác ABE = tam giác ACD (c-g-c)
=> BE=CD ( cặp cạnh t/ứng)
=> góc ABE=góc ACD (cặp góc t/ứng) hay góc ABK=góc ACK
b) Vì AB=AC, AD=AE => BD=CE( vì AD+BD=AB;AE+EC=AC)
tam giác DBK có: góc D+góc B+góc K=180 độ
tam giác KCE có: góc K+góc C+góc E=180 độ
mà Góc B= góc C(cmt) và Góc K1=Góc K1(đối đỉnh)---bạn tự kí hiệu nha :")
=> góc D=góc E
Xét tam giác BKD và tam giác KCE, ta có:
Góc BDK=góc KEC(cmt)
Góc DBK=góc ECK(cmt)
DB=CE(cmt)
Vậy tam giác BKD = tam giác KCE(g-c-g)
=> DK=EK(cặp cạnh tướng ứng)
c) Xét tam giác ADK và tam giác AEK, ta có:
AD=AE(gt)
DK=KE(cmt)
AK là cạnh chung
Vậy tam giác ADK= tam giác AEK(c-c-c)
=> góc DAK=góc EAK(cặp góc t/ứng) hay góc BAK=góc CAK
=> AK là p/g của góc BAC
d) Góc BAK=góc CAK hay góc BAI=góc CAI
Xét tam giác BAI và tam giác CAI, ta có:
AB=AC(gt)
AI là cạnh chung
Góc BAI=góc CAI (cmt)
Vậy tam giác BAI = tam giác CAI(c-g-c)
=>Góc AIB=góc AIC(cặp góc t/ứng)
mà góc AIB+góc AIC=180 độ => AIB=AIC=90 độ
=> AI vuông góc với BC

a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Xét ΔDBC và ΔECB có
DB=EC
BC chung
DC=EB
Do đó: ΔDBC=ΔECB
Xét ΔKBD và ΔKCE có
\(\widehat{KBD}=\widehat{KCE}\)
BD=CE
\(\widehat{KDB}=\widehat{KEC}\)
Do đó:ΔKBD=ΔKCE

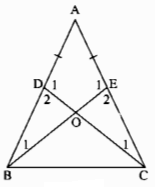
a) Xét ∆BEA và ∆CDA, ta có:
BA = CA (gt)
\(\widehat{A}\)chung
AE = AD (gt)
Suy ra: ∆BEA = ∆CDA (c.g.c)
Vậy BE = CD (hai cạnh tương ứng)
b) ∆BEA = ∆CDA (chứng minh trên)
⇒\(\widehat{\text{B1}}=\widehat{\text{C1}}\);\(\widehat{\text{E1}}=\widehat{\text{D1}}\) (hai góc tương ứng)
\(\widehat{\text{E1}}+\widehat{\text{E2}}\)=180o (hai góc kề bù)
\(\widehat{\text{D1}}+\widehat{\text{D2}}\)=180o (hai góc kề bù)
Suy ra: \(\widehat{\text{E2}}=\widehat{\text{D2}}\)
AB = AC (gt)
⇒ AE + EC = AD + DB mà AE = AD (gt) => EC = DB
Xét ∆ODB và ∆OCE, ta có:
\(\widehat{\text{E2}}=\widehat{\text{D2}}\) (chứng minh trên)
DB = EC (chứng minh trên)
\(\widehat{\text{B1}}=\widehat{\text{C1}}\)(chứng minh trên)
Suy ra: ∆ODB = ∆OEC (g.c.g)

A B K C D E
a) Xét \(\Delta ABE\) và \(\Delta ACD\)
có: + AE=AD(gt)
+A: là góc chung
+AB=AC(do \(\Delta ABC\) cân tại A)
Vậy \(\Delta ABE\)=\(\Delta ACD\) (c.g.c)
=> BE=CD( 2 cạnh tương ứng)
b) Vì \(\Delta ABE\) =\(\Delta ACD\) (cmt)
nên: góc ABE=góc ACD( 2 góc tương ứng)
c) .\(\Delta KBC\) cân tại K
. Ta có: góc B = \(B_1+B_2\)
C=\(C_1=C_2\)
B=C(gt);\(B_1=C_1\) (cmt)
=> \(B_2=C_2\)
Do đó \(\Delta KBC\) cân tại K

a, Xét ΔABE=ΔACD
có: AB=AC
^A là góc chung
AD=AE
==> ΔABE=ΔACD(c-g-c)
b, Xét ΔKBD và ΔKCE
^K1=^K2 (đđ)
BD=CE( AB=AC và AD=AE)
KD=KE
==> ΔKBD=ΔKCE (c-g-c)
c, Xét ΔAKB và ΔAKC
có AK cạnh chung
KB=KC
AB=AC
=>ΔAKB = ΔAKC (c-c-c)
=> ^BAK= ^CAK mà AK là cạnh chung
=> AK là tia phân giác của góc BAC

a) xét \(\Delta\)ABH và\(\Delta\)AHC có:AH chung. BH=HC.AB=AC=>bằng nhau ccc=>góc AHC =góc AHB
mà AHB + AHC =180 độ => góc AHB=AHC=90độ (đpcm)
b)ta thấy góc ABC+CBD=180độ;góc ACB+BCE=180độ=>góc CBD=BCE(kề bù vs 2 góc băng nhau)
xét \(\Delta\)DBC và\(\Delta\)BCE có :BD=CE,góc CBD=BCE,BC chung =>góc D= E,góc DCB=DBC=>góc DBK=ECK(vì góc DBC=ECB)
xét \(\Delta\)DBK và EKC có góc D=E,BD=CE,góc DBK=ECK=>bằng nhau gcg
a/ Xét tam giác BCD và tam giác BCE có
-góc B = góc C
-BD = EC
-BC: cạnh chung
=> tam giác BCD = tam giác BCE (cạnh góc cạnh)
=> BE=CD (2 cạnh tương ứng)
b/ Xét tam giác KBD và tam giác KCE có
-Góc BKD = góc CKE (đối đỉnh)
-BD=CE
-KB=KC
=> tam giác KBD = tam giác KCE
ở câu a tại sao góc b= góc c vậy bn