Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Xét tam giác BCD và tam giác BCE có
-góc B = góc C
-BD = EC
-BC: cạnh chung
=> tam giác BCD = tam giác BCE (cạnh góc cạnh)
=> BE=CD (2 cạnh tương ứng)
b/ Xét tam giác KBD và tam giác KCE có
-Góc BKD = góc CKE (đối đỉnh)
-BD=CE
-KB=KC
=> tam giác KBD = tam giác KCE

Bài giải
A B C D E K
a, Xét \(\Delta AEB\) và \(\Delta ADC\) , có :
\(AD=AE\) ( giả thiết )
\(\widehat{A}\) : góc chung
\(AB=AC\) ( giả thiết )
\(\Rightarrow\text{ }\Delta AEB=\Delta ADC\) \(\left(c\text{ - }g\text{ - }c\right)\)
\(\Rightarrow\text{ }BE=CD\text{ ( cạnh tương ứng )}\)
b, AB = AC , AD = AE => AB - AD = AC - AE hay DB = EC
Xét \(\Delta BCD\)và \(\Delta CBE\)có:
BC : cạnh chung
CD = BE ( chứng minh trên )
BD = CE ( chứng minh trên )
\(\Rightarrow\text{ }\Delta BCD=\Delta CBE\text{ }\left(c\text{ - }c\text{ - }c\right)\)
\(\Rightarrow\text{ }\widehat{ BDC}=\widehat{\text{ CEB}}\)( hai góc tương ứng )
Xét \(\Delta KBD\) và \(\Delta KCE\)có:
\(\widehat{BDC}=\widehat{CEB}\)( chứng minh trên )
BD = CE ( chứng minh trên )
\(\widehat{ABK}=\widehat{ACK}\) ( 2 góc tương ứng do \(\Delta ABE=\Delta ACD\) )
\(\Rightarrow\text{ }\Delta KBD=\Delta KCE\left(g\text{ - }c\text{ - }g\right)\)

tự vẽ hình
a) Xét tam giác ABE và tam giác ACD, ta có:
Góc BAE= góc DAC(hay góc A là góc chung)
AD=AC(gt)
AD=AE(gt)
Vậy tam giác ABE = tam giác ACD (c-g-c)
=> BE=CD ( cặp cạnh t/ứng)
=> góc ABE=góc ACD (cặp góc t/ứng) hay góc ABK=góc ACK
b) Vì AB=AC, AD=AE => BD=CE( vì AD+BD=AB;AE+EC=AC)
tam giác DBK có: góc D+góc B+góc K=180 độ
tam giác KCE có: góc K+góc C+góc E=180 độ
mà Góc B= góc C(cmt) và Góc K1=Góc K1(đối đỉnh)---bạn tự kí hiệu nha :")
=> góc D=góc E
Xét tam giác BKD và tam giác KCE, ta có:
Góc BDK=góc KEC(cmt)
Góc DBK=góc ECK(cmt)
DB=CE(cmt)
Vậy tam giác BKD = tam giác KCE(g-c-g)
=> DK=EK(cặp cạnh tướng ứng)
c) Xét tam giác ADK và tam giác AEK, ta có:
AD=AE(gt)
DK=KE(cmt)
AK là cạnh chung
Vậy tam giác ADK= tam giác AEK(c-c-c)
=> góc DAK=góc EAK(cặp góc t/ứng) hay góc BAK=góc CAK
=> AK là p/g của góc BAC
d) Góc BAK=góc CAK hay góc BAI=góc CAI
Xét tam giác BAI và tam giác CAI, ta có:
AB=AC(gt)
AI là cạnh chung
Góc BAI=góc CAI (cmt)
Vậy tam giác BAI = tam giác CAI(c-g-c)
=>Góc AIB=góc AIC(cặp góc t/ứng)
mà góc AIB+góc AIC=180 độ => AIB=AIC=90 độ
=> AI vuông góc với BC

Ta có hình vẽ:
A B C K D E
Xét Δ ABE và Δ ACD có:
AB = AC (gt)
A là góc chung
AE = AD (gt)
Do đó, Δ ABE = Δ ACD (c.g.c)
=> ABE = ACD (2 góc tương ứng)
và AEB = ADC (2 góc tương ứng)
Mà AEB + BEC = 180o (kề bù)
ADC + CDB = 180o (kề bù)
nên BEC = CDB
Có: AB = AC (gt)
AD = AE (gt)
=> AB - AD = AC - AE
=> BD = CE
Xét Δ KBD và Δ KCE có:
KBD = KCE (cmt)
BD = CE (cmt)
KDB = KEC (cmt)
Do đó, Δ KBD = Δ KCE (đpcm)
Ta có hình vẽ:
A B C D E K Xét tam giác ABE và tam giác ACD có:
A: góc chung
AB = AC (GT)
AD = AE (GT)
=> tam giác ABE = tam giác ACD (c.g.c)
=> \(\widehat{B}\)=\(\widehat{C}\) (2 góc tương ứng) (1)
=> \(\widehat{ADC}\)=\(\widehat{AEB}\) (2 góc tương ứng) (*)
Mà \(\widehat{ADC}\)+\(\widehat{CDB}\)=1800 (kề bù) (**)
và \(\widehat{AEB}\)+\(\widehat{BEC}\)=1800 (kề bù) (***)
Từ (*),(**),(***) => \(\widehat{KDB}\)=\(\widehat{KEC}\) (2)
Ta có: AB = AC; AD = AE => DB=EC (3)
Từ (1);(2);(3) => tam giác KBD = tam giác KCE (đpcm)

a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Xét ΔDBC và ΔECB có
DB=EC
BC chung
DC=EB
Do đó: ΔDBC=ΔECB
Xét ΔKBD và ΔKCE có
\(\widehat{KBD}=\widehat{KCE}\)
BD=CE
\(\widehat{KDB}=\widehat{KEC}\)
Do đó:ΔKBD=ΔKCE

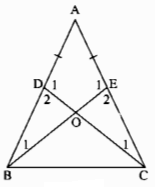
a) Xét ∆BEA và ∆CDA, ta có:
BA = CA (gt)
\(\widehat{A}\)chung
AE = AD (gt)
Suy ra: ∆BEA = ∆CDA (c.g.c)
Vậy BE = CD (hai cạnh tương ứng)
b) ∆BEA = ∆CDA (chứng minh trên)
⇒\(\widehat{\text{B1}}=\widehat{\text{C1}}\);\(\widehat{\text{E1}}=\widehat{\text{D1}}\) (hai góc tương ứng)
\(\widehat{\text{E1}}+\widehat{\text{E2}}\)=180o (hai góc kề bù)
\(\widehat{\text{D1}}+\widehat{\text{D2}}\)=180o (hai góc kề bù)
Suy ra: \(\widehat{\text{E2}}=\widehat{\text{D2}}\)
AB = AC (gt)
⇒ AE + EC = AD + DB mà AE = AD (gt) => EC = DB
Xét ∆ODB và ∆OCE, ta có:
\(\widehat{\text{E2}}=\widehat{\text{D2}}\) (chứng minh trên)
DB = EC (chứng minh trên)
\(\widehat{\text{B1}}=\widehat{\text{C1}}\)(chứng minh trên)
Suy ra: ∆ODB = ∆OEC (g.c.g)
bạn có thể xem ở bạn LÊ YẾN NHI
mình đã trả lời cho bạn đó
bạn lên app QuandA hỏi nha, gia sư sẽ cho bạn đáp án chính xác