Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=MB=MC=\dfrac{BC}{2}\)
Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
nên AMCK là hình bình hành
Hình bình hành AMCK có MA=MC
nên AMCK là hình thoi
b: AMCK là hình thoi
=>AK//MC và AK=MC
AK//MC
M\(\in\)BC
Do đó: AK//MB
AK=MC
MC=MB
Do đó: AK=MB
Xét tứ giác AKMB có
AK//MB
AK=MB
Do đó: AKMB là hình bình hành
c; Để hình thoi AMCK trở thành hình vuông thì \(\widehat{KCM}=90^0\)
AMCK là hình thoi
=>CA là phân giác của \(\widehat{KCM}\)
=>\(\widehat{ACM}=\dfrac{1}{2}\cdot\widehat{KCM}=45^0\)
=>\(\widehat{ACB}=45^0\)

a: Xét ΔABC có
M,I lần lượt là trung điểm của CB,CA
=>MI là đường trung bình
=>MI//AB và MI=AB/2
mà MI=MK/2
nên MK=AB
MI//AB
AB vuông góc AC
=>MI vuông góc AC
Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
=>AMCK là hình bình hành
mà AC vuông góc MK
nên AMCK là hình thoi
b: Xét tứ giác AKMB có
MK//AB
MK=AB
=>AKMB là hình bình hành

a: ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(MA=MC=MB=\dfrac{BC}{2}\)
Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
=>AMCK là hình bình hành
Hình bình hành AMCK có MA=MC
nên AMCK là hình thoi
b: AMCK là hình thoi
=>AK//MC và AK=MC
AK=MC
MB=MC
Do đó: AK=MB
AK//MC
M\(\in\)BC
Do đó: AK//MB
Xét tứ giác ABMK có
AK//BM
AK=BM
Do đó: ABMK là hình bình hành
=>AM cắt BK tại trung điểm của mỗi đường
mà O là trung điểm của AM
nên O là trung điểm của BK
=>B,O,K thẳng hàng

a: Xét ΔABC có
M,I lần lượt là trung điểm của CB,CA
=>MI là đường trung bình của ΔABC
=>MI//AB và MI=AB/2
MI//AB
\(I\in MK\)
Do đó: MK//AB
\(MI=\dfrac{AB}{2}\)
\(MI=\dfrac{MK}{2}\)
Do đó: AB=MK
Xét tứ giác ABMK có
MK//AB
MK=AB
Do đó: ABMK là hình bình hành
b: Để hình bình hành AKMB là hình thoi thì MB=BA
ΔABC vuông tại A có AM là đường trung tuyến
nên \(AM=MB=MC=\dfrac{BC}{2}\)
=>AM=MB=BA
=>ΔMAB đều
=>\(\widehat{ABC}=60^0\)

a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trung điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật


a) Tam giác ABC cân tại A có AM là đường trung tuyến
=> AM cũng là đường cao
=> AM⊥BC
Tứ giác AMCK có : I là trung điểm của đường chéo MK
I là trung điểm của đường chéo AC
=> AMCK là hình bình hành
mà góc AMC bằng 90 độ
=> AMCK là hình chữ nhật
b) Ta có: AK =MC ( 2 cạnh đối trong hình chữ nhật)
mà MC=MB ( M là trung điểm của BC)
=> AK=MB
Ta có: AK//MC( 2 cạnh đối trong hình chữ nhật)
mà MC và MB là 2 tia đối
=> AK//MB
Tứ giác AKBM có: AK=MB
AK//MB
=> AKBM là hình bình hành
c) Tứ giác ABEC có: M là trung điểm của đường chéo AE
M là trung điểm của đường chéo BC
=> ABEC là hình bình hành
mà AE⊥BC( cmt)
=> ABEC là hình thoi

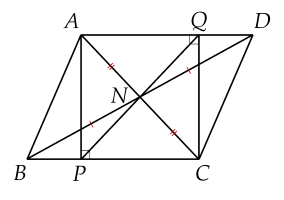
a) ����ABCD là hình bình hành.
b) �,�,�P,N,Q thẳng hàng.
c) Δ���ΔABC cần thêm điều kiện gì để tứ giác ����ABCD là hình vuông.

của cj nó
Thấy tao thông minh chưa hả ? Học tập theo tao nè

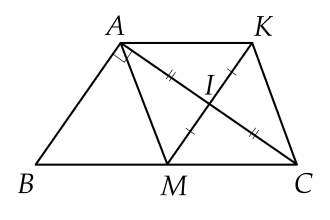
a/
Ta có
IA=IC (gt); IM=IK (gt) => AMCK là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Ta có
MB=MC (gt); IA=IC (gt) => MI là đường trung bình của tg ABC => MI//AB
Mà \(AB\perp AC\)
\(\Rightarrow MI\perp AC\Rightarrow MK\perp AC\)
=> AMCK là hình thoi (Hình bình hành có 2 đường chéo vuông góc là hình thoi)
b/
Ta có
MI//AB (cmt) => MK//AB
AK//MC (cạnh đối hbh AMCK) => AK//MB
=> AKMB là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
c/
Để AMCK là hình vuông \(\Rightarrow AM\perp BC\) => AM là đường cao của tg ABC
Mà AM là trung tuyến của tg ABC (gt)
=> ABC cân tại A (Tam giác có đường cao đồng thời là đường trung tuyến là tg cân)
=> Để AMCK là hình vuông thì tg ABC vuông cân tại A
a) Tứ giác ����AMCK có hai đường chéo ��,��AC,MK cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
Δ���ΔABC vuông tại �A có ��AM là đường trung tuyến nên ��=��=��AM=MC=MB.
Vậy hình bình hành ����AMCK có ��=��AM=MC nên là hình thoi.
b) Vì ����AMCK là hình thoi nên ��AK // ��BM và ��=��=��AK=MC=BM.
Tứ giác ����AKMB có ��AK // ��,��=��BM,AK=BM nên là hình bình hành.
c) Để ����AMCK là hình vuông thì cần có một góc vuông hay ��⊥��AM⊥MC.
Khi đó Δ���ΔABC có ��AM vừa là đường cao vừa là đường trung tuyến nên cân tại �A.
Vậy Δ���ΔABC vuông cân tại �A thì ����AMCK là hình vuông.