Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

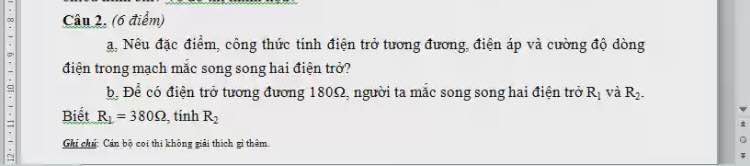
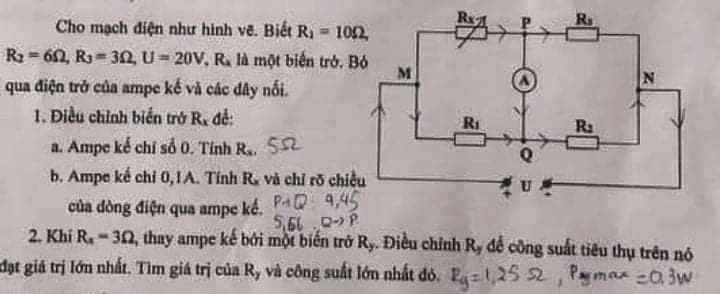
\(R1ntR2\Rightarrow P2=U2.I2=I2^2R2=Im^2.R2\)
\(\Rightarrow P2=\left(\dfrac{Um}{Rtd}\right)^2.R2=\left(\dfrac{12}{R1+R2}\right)^2.R2\)
\(\Rightarrow P2=\dfrac{12^2.R2}{\left(R1+R2\right)^2}=\dfrac{144R2}{\left(6+R2\right)^2}=\dfrac{144}{\dfrac{\left(6+R2\right)^2}{\sqrt{R2}^2}}=\dfrac{144}{\left(\dfrac{6}{\sqrt{R2}}+\sqrt{R2}\right)^2}\)
\(\Rightarrow\left(\dfrac{6}{\sqrt{R2}}+\sqrt{R2}\right)^2\ge\left(2\sqrt{6}\right)^2\ge24\left(AM-GM\right)\)
\(\Rightarrow P2=\dfrac{144}{\left(\dfrac{6}{\sqrt{R2}}+\sqrt{R2}\right)^2}\le\dfrac{144}{24}\le6W\Rightarrow P2max=6W\)
\(dấu\) \("="\) \(xảy\) \(ra\Leftrightarrow\dfrac{6}{\sqrt{R2}}=\sqrt{R2}\Leftrightarrow R2=6\Omega\)

a. Ta có
P = m g = 1 , 5.10 = 150 ( N )
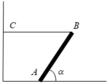
Theo điều kiện cân bằng của vật rắn quay quanh trục A:
M T = M P ⇒ T . d T = P . d P ⇒ T . A B . sin α = P . A B 2 . cos α ( * ) ⇒ T = 150. 1 2 . 1 2 3 2 = 25 3 ( N )

Chọn hệ quy chiếu Oxy như hình vẽ
Theo điều kiện cân bằng của vật rắn
P → + N → + f → m s + T → = 0 →
Chiếu (1) lên Ox
f m s − T = 0 ⇒ f m s = 25 3 ( N )
Chiếu (1) lên Oy
P − N = 0 ⇒ N = P = 150 ( N )
b. Từ ( * ) ta có T = P . cotg α 2
Lúc này F → m s là lực ma sát nghỉ
⇒ F m s ≤ k N ⇒ 1 2 m g . cot g α ≤ k . m g ⇒ cot g α ≤ 2 k = 3 ⇒ α ≥ 30 0

\(\dfrac{Gm_1}{d_1^2}=\dfrac{Gm_2}{d_2^2}\Rightarrow d_2=4d_1\)
Vì vậy để lực tác dụng của m1 và m2 lên m3 bằng nhau thì chỉ cần tìm vị trí sao cho d2=4d1.
Còn để lực tác dụng lên m3 làm cho m3 cân bằng thì m3 phải nằm trong AB. Lúc này, d1, d2 thỏa mãn
\(\left\{{}\begin{matrix}d_2=4d_1\\d_2+d_1=36R_1\end{matrix}\right.\)Giải ra d1= 7,2 R1

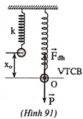
a) Khi m ở vị trí cân bằng O: P → + F d h → = 0 →
Về độ lớn: m g - k x 0 = 0 1
Trong đó x0 là độ giãn lò xo khi vật ở vị trí cân bằng (hình 91). Xét khi m chuyển động, ở vị trí cách O một đoạn x. Thế năng của hệ sẽ bằng công do trọng lực và lực đàn hồi thực hiện khi m di chuyển từ vị trí đang xét trở về vị trí ban đầu ( tức là trở về vị trí cân bằng O).
Ta có:
![]()
hay
![]()
Từ (1) và (2)
![]()
b) Tại vị trí ban đầu ta có
![]()

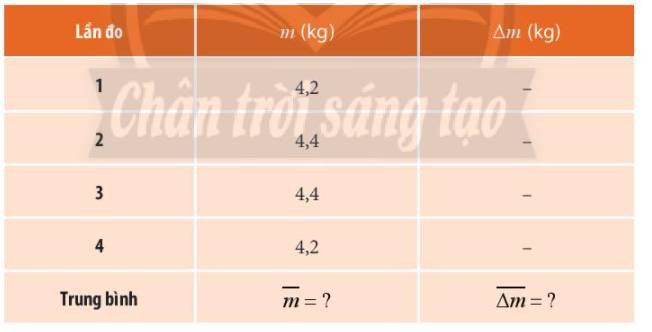
Giá trị trung bình khối lượng của túi trái cây là:
\(\overline m = \frac{{{m_1} + {m_2} + {m_3} + {m_4}}}{4} = \frac{{4,2 + 4,4 + 4,4 + 4,2}}{4} = 4,3(kg)\)
Sai số tuyệt đối ứng với mỗi lần đo là:
\(\begin{array}{l}\Delta {m_1} = \left| {\overline m - {m_1}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\\\Delta {m_2} = \left| {\overline m - {m_2}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_3} = \left| {\overline m - {m_3}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_4} = \left| {\overline m - {m_4}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\end{array}\)
Sai số tuyệt đối trung bình của phép đo:
\(\overline {\Delta m} = \frac{{\Delta {m_1} + \Delta {m_2} + \Delta {m_3} + \Delta {m_4}}}{4} = \frac{{0,1 + 0,1 + 0,1 + 0,1}}{4} = 0,1(kg)\)
Sai số tuyệt đối của phép đo là:
\(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = 0,1 + 0,1 = 0,2(kg)\)
Sai số tương đối của phép đo là:
\(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = \frac{{0,2}}{{4,2}}.100\% = 4,65\% \)
Kết quả phép đo:
\(m = \overline m \pm \Delta m = 4,3 \pm 0,2(kg)\)