Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\left(\frac{v}{x}\right)'=\frac{v^2-ax}{v^2}\)
Mà: \(a=-\omega^2x\) nên \(\left(\frac{v}{x}\right)'=1+\frac{\omega^2x}{v^2}=1+\frac{x^2}{\frac{v^2}{\omega^2}}=1+\frac{x^2}{A^2-x^2}\)
Đạo hàm 2 vế biểu thức đã cho ta có:
\(1+\frac{x_1^2}{A^2-x_1^2}+1+\frac{x_2^2}{A^2-x_2^2}=1+\frac{x_3^2}{A^2-x_3^2}\)
Thay số vào ta tìm đc giá trị \(x_0\)

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

Đáp án A
+ Xét đạo hàm sau:
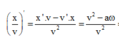
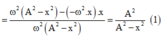
+ Xét biểu thức x 1 v 1 + x 2 v 2 = x 3 v 3
+ Lấy đạo hàm hai vế và áp dụng đạo hàm (1) ta có:
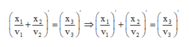
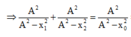
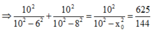
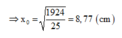

+ Xét đạo hàm sau:
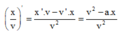
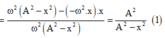
+ Xét biểu thức: x 1 v 1 + x 2 v 2 = x 3 v 3
+ Lấy đạo hàm hai vế và áp dụng đạo hàm (1) ta có:
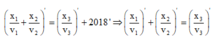
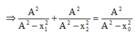
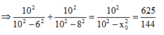
⇒ x 0 = 1924 25 = 8 , 77 ( c m )

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm
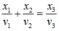
 chọn A
chọn A
Đáp án C
Phương pháp: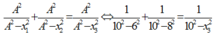
Cách giải:
Ta có: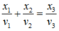
Đạo hàm hai vế của phương trình theo t ta được: