Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tần số dao động riêng: \(f=\frac{1}{2\pi\sqrt{LC}}\Rightarrow\frac{1}{f^2}=k.C\)(Vì chỉ thay đổi C nên ta biểu diễn f theo C, k là một hệ số nào đó)
Suy ra:
\(\frac{1}{f_1^2}=k.C_1\)
\(\frac{1}{f_2^2}=k.C_2\)
Ta cần tìm:
\(\frac{1}{f^2}=k\left(C_1+C_2\right)\Rightarrow\frac{1}{f^2}=kC_1+kC_2\)
\(\Rightarrow\frac{1}{f^2}=\frac{1}{f_1^2}+\frac{1}{f_2^2}\)
Thay số ta đc f = 35Hz
Mạch chỉ có tụ điện (hoặc cuộn cảm) thì u vuông pha với i
\(\Rightarrow\left(\frac{u}{U_0}\right)^2+\left(\frac{i}{I_0}\right)^2=1\)
Đáp án là D, vì hai điểm trên dây dao động ngược pha thì cách nhau: (k+0,5)λ
Giả sử cuộn dây không thuần cảm, có điện trở r.
Giả thiết có vẻ thiếu gì đó, bạn kiểm tra lại xem. Hoặc chỉ cần vẽ giản đồ véc tơ thì thấy cuộn dây không thuần cảm vẫn OK.
Zc Z Z r R d m L Z
BONUS thêm bạn cách biến đổi đại số
Ta có Im = Id suy ra Zm = Zđ \(\Leftrightarrow R^2+Z_C^2=\left(R+r\right)^2+\left(Z_L-Z_C\right)^2\)(*)
id sớm pha \(\frac{\pi}{2}\)so với im nên \(\tan\varphi_đ\tan\varphi_m=-1\Leftrightarrow\frac{-Z_C}{R}.\frac{Z_L-Z_C}{R+r}=-1\)
\(\Rightarrow Z_L-Z_C=\frac{R\left(R+r\right)}{Z_C}\)(**)
Thế vào (*) ta có: \(R^2+Z_C^2=\left(R+r\right)^2+\left(R+r\right)^2\frac{R^2}{Z_C^2}\)
\(\Leftrightarrow R^2+Z_C^2=\left(R+r\right)^2\frac{R^2+Z_C^2}{Z_C^2}\Leftrightarrow R+r=Z_C\)(1)
Thế vào (**) ta đc: \(Z_L-Z_C=R\) (2)
Hai phương trình (1) và (2) vẫn chưa thể kết luận r = 0.
Áp dụng công thức: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow A^2=2,5^2+\dfrac{(50\sqrt 3)^2}{\omega^2}=(2,5\sqrt 3)^2+\dfrac{50^2}{\omega^2}\)
\(\Rightarrow \omega = 20(rad/s)\)
Và \(A=5cm\)
Do mạch chỉ có L nên u và i luôn vuông pha nhau.
Phương trình của i có dạng: (1)
và Phương trình của i có dạng: (2)
Từ (1) và (2) suy ra
Ta có hệ :
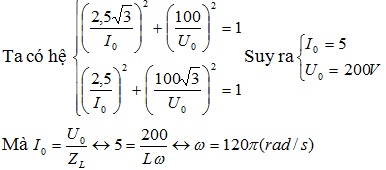
\(v = -120\cos (20t) = 120\sin(20t-\frac{\pi}{2}).\)
\(\omega = 20 \)(rad/s) ; \(A = \frac{v_{max}}{\omega} = 6cm.\)=> \(T = \frac{2\pi}{\omega} = \frac{\pi}{10} s .\)
Li độ trễ pha hơn vận tốc là \(\pi/2\)=> \(x = 6 \sin(20t-\pi).\)
tại \(t = T/6\) => \(x = 6 \sin(20\frac{T}{6}-\pi) = 6 \sin (\frac{\pi}{3}-\pi)=-3\sqrt{3} cm.\)
Chọn đáp án.D.
Đáp án C
Phương pháp: 
Cách giải:
Ta có: 
Đạo hàm hai vế của phương trình theo t ta được:
Ta có: \(\left(\frac{v}{x}\right)'=\frac{v^2-ax}{v^2}\)
Mà: \(a=-\omega^2x\) nên \(\left(\frac{v}{x}\right)'=1+\frac{\omega^2x}{v^2}=1+\frac{x^2}{\frac{v^2}{\omega^2}}=1+\frac{x^2}{A^2-x^2}\)
Đạo hàm 2 vế biểu thức đã cho ta có:
\(1+\frac{x_1^2}{A^2-x_1^2}+1+\frac{x_2^2}{A^2-x_2^2}=1+\frac{x_3^2}{A^2-x_3^2}\)
Thay số vào ta tìm đc giá trị \(x_0\)
Em hiểu thế này có đúng không ạ? Tại em biến đổi phương trình đầu tiên của nhưng mà không có ra?
\((\frac{x}{v})' = \frac{x'.v - v'.x}{v^2}= \frac{v^2-ax}{v^2}\)
hay là
\((\frac{v}{x})'= \frac{ax - x^2}{v^2}\)