
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

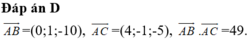

Đáp án D
Phương pháp giải: Xét đẳng thức vectơ, đưa về hình chiếu của điểm trên mặt phẳng
Lời giải:
Gọi M(a;b;c) thỏa mãn đẳng thức vectơ
![]()
=2(1-a;1-b;1-c)+(0-a; 1-b;2-c)+(-2-1;1-b;4-c)=0
![]()
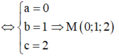
Khi đó
![]()
![]()
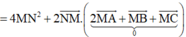
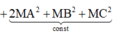
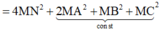
![]()
<=> N là hình chiếu của M trên (P) =>MN ⊥ (P)
Phương trình đường thẳng MN là
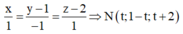
![]()
![]()
![]()

Phương trình hoành độ giao điểm
x3+2mx2+3(m-1)x+2 =-x+2 hay x(x2+2mx+3(m-1))=0
suy ra x=0 hoặc x2+2mx+3(m-1)=0 (1)
Đường thẳng d cắt (C) tại ba điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác 0
⇔ m 2 - 3 m + 3 > 0 m - 1 ≠ 0 ⇔ ∀ m m ≠ 1 ⇔ m ≠ 1
Khi đó ta có: C( x1 ; -x1+2) ; B(x2 ; -x2+2) trong đó x1 ; x2 là nghiệm của (1) ; nên theo Viet thì x 1 + x 2 = - 2 m x 1 x 2 = 3 m - 3
Vậy
C B → = ( x 2 - x 1 ; - x 2 + x 1 ) ⇒ C B = 2 ( x 2 - x 1 ) 2 = 8 ( m 2 - 3 m + 3 )
d ( M ; ( d ) ) = - 3 - 1 + 2 2 = 2
Diện tích tam giác MBC bằng khi và chỉ khi
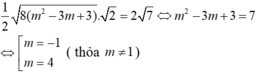
Chọn B.

Chọn A.
![]()
Để 3 điểm A, B, C thẳng hàng khi và chi khi A B → , A C → cùng phương
![]()