
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Gọi vector pháp tuyến của \((P)\) là \((a,b,c)\)
Ta có \((-1,-2,3)=\overrightarrow {AB}\perp \overrightarrow{n_P}\Rightarrow -a-2b+3c=0\) $(1)$
Do mặt phẳng đi qua \(A\) nên nó có dạng:\(a(x-1)+by+cz=0\)
Khoảng cách từ \(C\mapsto (P)\) là : \(d=\frac{|b+c|}{\sqrt{a^2+b^2+c^2}}=\frac{2}{\sqrt{3}}\)
\(\Rightarrow 6bc=4a^2+b^2+c^2\) $(2)$
Từ \((1),(2)\Rightarrow 6bc=4(2b-3c)^2+b^2+c^2\Leftrightarrow 17b^2+37c^2-54bc=0\)
\(\Leftrightarrow (37c-17b)(c-b)=0\)
TH1: \(b=c\Rightarrow a=3c-2b=b\)
PTMP: \(b(x-1)+by+bz=0\Leftrightarrow x+y+z-1=0\)
TH2: \(c=\frac{17b}{37}\Rightarrow a=3c-2b=\frac{-23}{37}b\)
PTMP: \(-\frac{23}{37}b(x-1)+by+\frac{17}{37}bz=0\Leftrightarrow \frac{-23}{37}x+y+\frac{17}{37}z+\frac{23}{37}=0\)

Đáp án D
Từ giả thiết ta suy ra
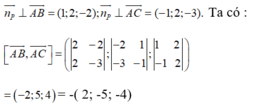
Từ đó suy ra n p → = (2; -5; -4) là một vectơ pháp tuyến của (P)

Chọn C

Ta có G(1;0;2), ta tìm hình chiếu của G lên mặt phẳng (P) bằng cách tìm giao điểm của đường thẳng qua G vuông góc với mặt phẳng (P) với mặt phẳng (P).
Phương trình đường thẳng qua điểm G và vuông góc với mặt phẳng (P)
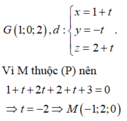

Ta có:
\(\overrightarrow{AB}=\left(-3;-2;2\right)\)\(\Rightarrow AB=\sqrt{\left(-3\right)^2+\left(-2\right)^2+2^2}=\sqrt{17}\)
\(\overrightarrow{BC}=\left(4;4;1\right)\Rightarrow BC=\sqrt{4^2+4^2+1^2}=\sqrt{33}\)
\(\overrightarrow{AC}=\left(1;2;3\right)\)\(\Rightarrow AC=\sqrt{1^2+2^2+3^2}=\sqrt{14}\)
\(\Rightarrow C_{\Delta ABC}=\sqrt{17}+\sqrt{33}+\sqrt{14}\)