K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
12 tháng 5 2017
Chọn C

Ta có G(1;0;2), ta tìm hình chiếu của G lên mặt phẳng (P) bằng cách tìm giao điểm của đường thẳng qua G vuông góc với mặt phẳng (P) với mặt phẳng (P).
Phương trình đường thẳng qua điểm G và vuông góc với mặt phẳng (P)
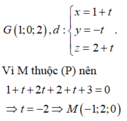

CM
9 tháng 11 2018
Đáp án B
Gọi I là trung điểm thỏa mãn
![]()
![]()
Khi đó
![]()
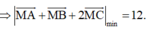
Dấu “=” xảy ra khi và chỉ khi
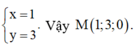

CM
29 tháng 10 2017
Đáp án A
Sử dụng phương trình mặt phẳng theo đoạn chắn, ta có phương trình mặt phẳng
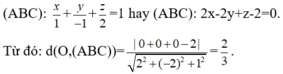

CM
22 tháng 3 2019
Chọn A.

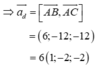
Đường thẳng d đi qua G(2;-1;0) và có vectơ chỉ phương là ![]()
Vậy phương trình tham số của d là 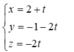

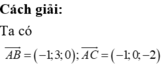



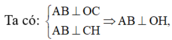
Lời giải:
Gọi vector pháp tuyến của \((P)\) là \((a,b,c)\)
Ta có \((-1,-2,3)=\overrightarrow {AB}\perp \overrightarrow{n_P}\Rightarrow -a-2b+3c=0\) $(1)$
Do mặt phẳng đi qua \(A\) nên nó có dạng:\(a(x-1)+by+cz=0\)
Khoảng cách từ \(C\mapsto (P)\) là : \(d=\frac{|b+c|}{\sqrt{a^2+b^2+c^2}}=\frac{2}{\sqrt{3}}\)
\(\Rightarrow 6bc=4a^2+b^2+c^2\) $(2)$
Từ \((1),(2)\Rightarrow 6bc=4(2b-3c)^2+b^2+c^2\Leftrightarrow 17b^2+37c^2-54bc=0\)
\(\Leftrightarrow (37c-17b)(c-b)=0\)
TH1: \(b=c\Rightarrow a=3c-2b=b\)
PTMP: \(b(x-1)+by+bz=0\Leftrightarrow x+y+z-1=0\)
TH2: \(c=\frac{17b}{37}\Rightarrow a=3c-2b=\frac{-23}{37}b\)
PTMP: \(-\frac{23}{37}b(x-1)+by+\frac{17}{37}bz=0\Leftrightarrow \frac{-23}{37}x+y+\frac{17}{37}z+\frac{23}{37}=0\)