Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

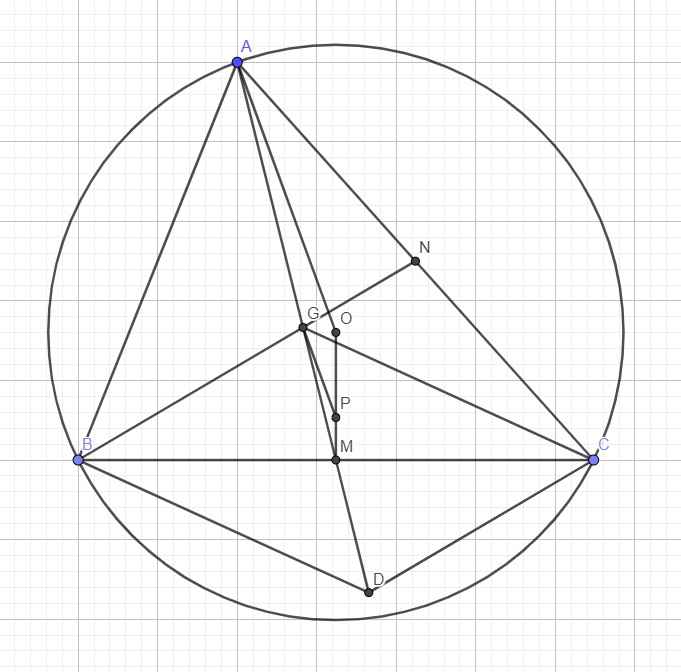
Nối OA, gọi M là trung điểm BC \(\Rightarrow\) OM cố định
Qua G kẻ đường thẳng song song OA cắt OM tại P
Trong tam giác OAM, theo định lý Talet:
\(\dfrac{GP}{OA}=\dfrac{PM}{OM}=\dfrac{GM}{AM}=\dfrac{1}{3}\)
Ta có những điều sau:
\(PM=\dfrac{1}{3}OM\) , mà O cố định, M cố định \(\Rightarrow\) P cố định
\(GP=\dfrac{1}{3}OA\Rightarrow GP=\dfrac{R}{3}\)
P cố định, độ dài \(\dfrac{R}{3}\) cố định
\(\Rightarrow\) Quỹ tích G là đường tròn (P) tâm P bán kính \(r=\dfrac{R}{3}\) (1)
Mặt khác BGCD là hình bình hành \(\Rightarrow\) D đối xứng G qua M (2)
(1);(2) \(\Rightarrow\) quỹ tích D là ảnh của đường tròn (P) qua phép đối xứng tâm M

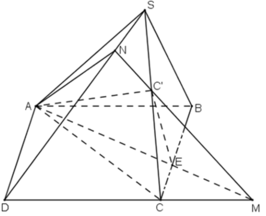
a) Giao điểm M của CD và mp(C’AE).
Trong mp(ABCD), d cắt CD tại M, ta có:
+ M ∈ CD
+ M ∈ d ⊂ (C’AE) ⇒ M ∈ (C’AE)
Vậy M là giao điểm của CD và mp(C’AE).
b) + Trong mặt phẳng (SCD), gọi giao điểm của MC’ và SD là N.
N ∈ MC’ ⊂ (C’AE) ⇒ N ∈ (C’AE).
N ∈ SD ⊂ (SCD) ⇒ N ∈ (SCD)
⇒ N ∈ (C’AE) ∩ (SCD).
⇒ (C’AE) ∩ (SCD) = C’N.
+ (C’AE) ∩ (SCB) = C’E.
+ (C’AE) ∩ (SAD) = AN.
+ (C’AE) ∩ (ABCD) = AE
Vậy thiết diện của hình chóp cắt bởi mặt phẳng (C’AE) là tứ giác C’NAE

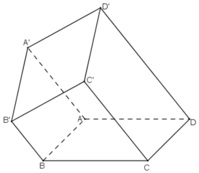
a) Giả sử (A’B’C’) ∩ d = D’
⇒ (A’B’C’) ∩ (C’CD) = C’D’.
+ AA’ // CC’ ⊂ (C’CD)
⇒ AA’ // (C’CD).
AB // CD ⊂ (CC’D)
⇒ AB // (CC’D)
(AA’B’B) có:
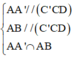 ⇒ (AA’B’B) // (C’CD).
⇒ (AA’B’B) // (C’CD).
Mà (A’B’C’) ∩ (AA’B’B) = A’B’
⇒ (A’B’C’) cắt (C’CD) và giao tuyến song song với A’B’
⇒ C’D’ // A’B’.
b) Chứng minh tương tự phần a ta có B’C’ // A’D’.
Tứ giác A’B’C’D’ có: B’C’ // A’D’ và C’D’ // A’B’
⇒ A’B’C’D’ là hình bình hành.
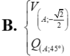
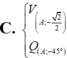
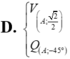

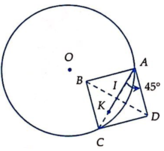

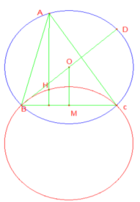
vẽ hình ta thấy
do tg ABCD là hình bình hành nên
\(\overrightarrow{AD}\)=\(\overrightarrow{BC}\)
Mà A,D cố định nên\(\Rightarrow\)\(\overrightarrow{AD}\) là vecto cố định
\(\Rightarrow\)T\(\overrightarrow{AD}\)(B)=C
Mà B thuộc (C) \(\Rightarrow\)C thuộc (C')là ảnh của (C) qua T\(\overrightarrow{AD}\)