Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Theo tính chất hình bình hành : BA=DC \(\Rightarrow\overrightarrow{AB}=\overrightarrow{CD}\). Nhưng theo giả thiết A,B cố định , cho nên \(\overrightarrow{AB}\) cố định . Ví C chạy trên (O;R) , D là ảnh của C qua phép tịnh tiến theo \(\overrightarrow{AB}\) , cho nên D chạy trên đường tròn O’ là ảnh của đường tròn O
- Cách xác định (O’) : Từ O kẻ đường thẳng // với AB , sau đó dựng véc tơ \(\overrightarrow{OO'}=\overrightarrow{AB}\). Từ O’ quay đường tròn bán kính R , đó chính là đường tròn quỹ tích của D.

Theo t/c đường tròn, do M là trung điểm BC \(\Rightarrow OM\perp BC\)
Áp dụng định lý Pitago:
\(OM=\sqrt{OC^2-CM^2}=\sqrt{R^2-\left(\dfrac{BC}{2}\right)^2}=3\)
\(\Rightarrow\) Quỹ tích M là đường tròn tâm \(\left(O;3\right)\)
Mặt khác do G là trọng tâm tam giác ABC
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
\(\Rightarrow\) G là ảnh của M qua phép vị tự tâm A tỉ số \(k=\dfrac{2}{3}\)
\(\Rightarrow\) Quỹ tích G là ảnh của \(\left(O;3\right)\) qua phép vị tự tâm A tỉ số \(k=\dfrac{2}{3}\)
\(\Rightarrow\) Quỹ tích G là đường tròn bán kính \(\dfrac{2}{3}.3=2\)

Đáp án B
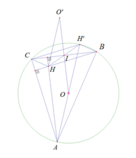
Gọi I là trung điểm BCH’ đối xứng với H qua I
( CH’ // BH do HBH’C là hình bình hành)
⇒ H ' C H ^ + H C M ^ = C H M ^ + H C M ^ = 90 o
(Cách chứng minh khác: Ta có C H ⊥ A B
Mà H’B//CH
⇒ H ' B ⊥ A B ⇒ H ' B C ^ = 90 o ⇒ H ' ∈ ( O )
Đ I : O-> O’
⇒ O H ' = O ' H
H thuộc đường tròn (O’; R)

Ta có vecto MM' + vecto MA = vecto MB
=> MM'BA là hình bình hành
vì A , B cố định => vecto AB cố định
xét phép tịnh tiến qua vecto AB biến M => M'
=> vecto MM' = vecto AB
=> M' là ảnh của M
Mặt khác điểm M chạy trên đường tròn (O) nên M' sẽ chạy trên đường tròn (O') là ảnh của
(O) thông qua phép tịnh tiến vecto AB
Vậy quỹ tích M' là đường tròn (O')

ta có : \(\overrightarrow{MM'}+\overrightarrow{MA}=\overrightarrow{MB}\Leftrightarrow\overrightarrow{MM'}=\overrightarrow{MB}-\overrightarrow{MA}=\overrightarrow{AB}\)
mà \(M\in\left(O\right)\Rightarrow M'\in\left(O'\right)\) với \(\left(O'\right)=T_{\overrightarrow{AB}}\left(O\right)\)
vậy tập hợp điểm \(M\) là đường tròn \(\left(O'\right)\) với \(\left(O'\right)\) là ảnh của đường tròn \(\left(O\right)\) qua \(T_{\overrightarrow{AB}}\)

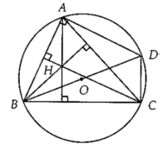
Nối OA, gọi M là trung điểm BC \(\Rightarrow\) OM cố định
Qua G kẻ đường thẳng song song OA cắt OM tại P
Trong tam giác OAM, theo định lý Talet:
\(\dfrac{GP}{OA}=\dfrac{PM}{OM}=\dfrac{GM}{AM}=\dfrac{1}{3}\)
Ta có những điều sau:
\(PM=\dfrac{1}{3}OM\) , mà O cố định, M cố định \(\Rightarrow\) P cố định
\(GP=\dfrac{1}{3}OA\Rightarrow GP=\dfrac{R}{3}\)
P cố định, độ dài \(\dfrac{R}{3}\) cố định
\(\Rightarrow\) Quỹ tích G là đường tròn (P) tâm P bán kính \(r=\dfrac{R}{3}\) (1)
Mặt khác BGCD là hình bình hành \(\Rightarrow\) D đối xứng G qua M (2)
(1);(2) \(\Rightarrow\) quỹ tích D là ảnh của đường tròn (P) qua phép đối xứng tâm M