

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




- Kẻ đường kính BB’ .Nếu H là trực tâm của tam giác ABC thì AH=B’C. Do C,B’ cố định , cho nên B’C là một véc tơ cố định \(\overrightarrow{\Rightarrow AH}=\overrightarrow{B'C}\)
Theo định nghĩa về phép tịnh tiến điểm A đã biến thành điểm H . Nhưng A lại chạy trên (O;R) cho nên H chạy trên đường tròn (O’;R) là ảnh của (O;R) qua phép tịnh tiến dọc theo \(\overrightarrow{v}=\overrightarrow{B'C}\)
- Cách xác định đường tròn (O’;R) . Từ O kẻ đường thẳng song song với B’C . Sau đó dựng véc tơ : \(\overrightarrow{OO'}=\overrightarrow{B'C}\). Cuối cùng từ O’ quay đường tròn bán kính R từ tâm O’ ta được đường tròn cần tìm .

- Kẻ AA’ ( là đường kính của (O) ) suy ra BHCA’ là hình bình hành , cho nên BC đi qua trung điểm I của A’H .
- A’H’ song song với BC ( vì cùng vuông góc với AH )
- Từ đó suy ra BC là đường trung bình của tam giác AHH’ – Có nghĩa là BC đi qua trung điểm của HH’ . Mặt khác AH vuông góc với BC suy ra BC là trục đối xứng của HH’ , hay H và H’ đối xứng nhau qua BC.
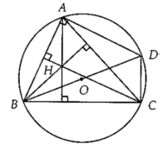
Gọi H là giao ba đường cao của tam giác ABC . Kéo dài AH cắt (O;R) tại H’ . Nối CH’
- Chứng minh IH=IH’ . Thật vậy
Ta có : \(\widehat{A}=\widehat{BCH'}\) ( Góc nội tiếp chẵn cung BH’ ).(1)
Mặt khác : \(\begin{cases}CH\perp AB\\CI\perp AH'\end{cases}\)\(\Rightarrow\widehat{A}=\widehat{BCH}\) (2)
Từ (1) và (2) suy ra : \(\widehat{BCH}=\widehat{BCH'}\)
Chứng tỏ tam giác HCH’ là tam giác cân . Do BC vuông góc với HH’ , chứng tỏ BC là đường trung trực của HH’ . Hay H và H’ đối xứng nhau qua BC . Cho nên khi A chạy trên đường tròn (O;R) thì H’ cũng chạy trên (O;R) và H sẽ chạy trên đường tròn (O’;R) là ảnh của đường tròn (O;R) qua phép đối xứng trục BC
- Giới hạn quỹ tích : Khi A trùng với B và C thì tam giác ABC suy biến thành đường thẳng . Vì thế trên đường tròn (O’;R) bỏ đi 2 điểm là ảnh của B,C

Phép quay tâm O, góc , biến I thành I'(0;
), phép vị tự tâm O, tỉ số
biến I' thành I'' = (0;
.
) = (0;2). Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc
và phép vị tự tâm O, tỉ số
biến đường tròn (I;2) thành đường tròn (I'';2
). Phương trình của đường tròn đó là
+
= 8
Phép quay tâm O, góc , biến I thành I'(0;
), phép vị tự tâm O, tỉ số
biến I' thành I'' = (0;
.
) = (0;2). Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc
và phép vị tự tâm O, tỉ số
biến đường tròn (I;2) thành đường tròn (I'';2
). Phương trình của đường tròn đó là
+
= 8

Ta thực hiện như sau:
Dựng \(\Delta'=Đ_1\left(\Delta\right)\)và giả sử \(\Delta'\) cắt \(\left(O;R\right)\) tại \(A\)
Nối \(IA\) cắt \(\Delta\) tại \(B\)
Khi đó \(I\) là trung điểm của đoạn thẳng \(AB\)
Bài toán chỉ có nghiệm khi đường thẳng \(\Delta'\)cắt đường tròn \(\left(O;R\right)\)

Gọi I' là ảnh của I qua phép biến hình nói trên
a) Phương trình của đường tròn (I;3) là ( +
= 9
b) (I) = I' (1;-1), phương trình đường tròn ảnh :
c) (I) = I'(3;2), phương trình đường tròn ảnh:
d) (I) = I'( -3;2), phương trình đường tròn ảnh:
Gọi I' là ảnh của I qua phép biến hình nói trên
a) Phương trình của đường tròn (I;3) là ( +
= 9
b) (I) = I' (1;-1), phương trình đường tròn ảnh :
c) (I) = I'(3;2), phương trình đường tròn ảnh:
d) (I) = I'( -3;2), phương trình đường tròn ảnh:

Vì : \(\overrightarrow{MN}=\overrightarrow{OA}\Rightarrow T_{\overrightarrow{OA}}:M\rightarrow N\). Do đó N nằm trên đường tròn ảnh của (O;R) . Mặt khác N lại nằm trên (O’;R’) do đó N là giao của đường tròn ảnh với với (O’;R’) . Từ đó suy ra cách tìm :
- Vè đường tròn tâm A bán kính R , đường tròn náy cắt (O’;R’) tại N
- Kẻ đường thẳng d qua N và song song với OA , suy ra d cắt (O;R) tại M

- Tam giác MPQ có QA là một đường cao , vì vậy nếu ta kẻ MM’ vuông góc với PQ thì MM’ cắt QA tại trực tâm H . OA là đường trung bình của tam giác MNH suy ra : \(\overrightarrow{MH}=2\overrightarrow{OA}=\overrightarrow{BA}\). Vậy phép tịnh tiến theo \(\overrightarrow{BA}\) biến điểm M thành điểm H . Nhưng M chạy trên (O;AB) cho nên H chạy trên đường tròn ảnh của (O;AB) qua phép tịnh tiến \(\overrightarrow{BA}\) .
- Tương tự đối với tam giác NPQ .
- Giới hạn quỹ tích . Do M không trùng với A,B cho nên trên đường tròn ảnh bỏ đi hai điểm ảnh của A,B => thỏa mãn yêu cầu bài toán .