Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

AMDB là hình thang
c/m":
goi AC giao voi BD tai I
tam giac MAC co IP la duong trung binh tam giac
=> IP // AM hay BD // AM (dpcm)
b/
vi AM // BD nen goc MAB = ABD (so le trong)
ma goc ABD = BAI (tam giac IAB can );
goi AM giao voi EF tai J
tam giac JAF can tai J
]=> goc MAB = JFA
=> JFA = IAB
=> EF // AC (2 goc so le tri\ong bang nhau )
ta can chung minh EP // AC nữa thi E; F; P thằng hàng do qua 1 diem co hai duong song song voi AC)
khi do ta chung minh EP la duong trung binh tam giac MCK ( K la giao cua ME va AC )
c/m E la trung diem cua KM
ta chung minh tam giac KAM can tai A
AE la duong cao (gt)
chung minh AE la phan giac
----- goc KAE = DAC ( doi dinh)
goc DAC = EAM ( cung phu voi goc MAB = IAB (cmt) )
=> AE dong thoi la phan giac
=> tam giac KAM can tai A
==>. dpcm
1) Vận tốc trung bình của người đó trên toàn bộ quãng đường AB là:
15 . \(\frac{1}{2}\) + 30 . \(\frac{1}{2}\)
\(\Rightarrow\) \(\frac{1}{2}\) . ( 15 + 30)
\(\Rightarrow\) \(\frac{1}{2}\) . 45
\(\Rightarrow\) 22,5

Câu 1:
Gọi x(km) là độ dài quãng đường AB (x > 0)
Thời gian ik là: \(\frac{x}{15}\left(h\right)\)
Thời gian về là: \(\frac{x}{12}\left(h\right)\)
Ta có PT: x/12 - x / 15 = 3/4
=> x = 45 (km)
Vậy ............
Câu 2:
(x2 – 6x + 9)2 -15(x2 – 6x + 10) = 1
Đặt x2 – 6x + 9 = t ≥ 0 => t2 - 15t - 16 = 0
t1 = -1(loại)
t2 = 16 => x2 – 6x + 9 = 16
x1 = 7; x1 = -1
S = {-1: 7}
#) Giải
Gọi thời gian đi là x ( h )
Thời gian về là \(x+\dfrac{3}{4}\left(h\right)\)
Quãng đường đi là 15.x ( km )
Quãng đường về là \(12\left(x+\dfrac{3}{4}\right)\left(km\right)\)
Theo đề bài ta có phương trình:
\(15.x=12\left(x+\dfrac{3}{4}\right)\)
x/12-x/15=3/4
⇔5x/60-4x/60=45/60
⇒5x-4x=45
⇒x=45
Vậy quãng đường AB dài 45km
~ Hok tốt ~

1. Thời gian đi với vận tốc 30km/giờ ít hơn thời gian đi với vận trốc 20 km/giớ là:
1 + 1 = 2 ( giờ )
Vận tốc trước so với vận tốc sau là:
30/20 = 3/2
Thời gian và vận tốc tỉ lệ nghịch với nhau.
Thời gian đi với vận tốc trước bằng 2/3 thời gian đi với vận tốc sau.
Thời gian đi với vận tốc 30km/giờ là:
2 x ( 3 – 2 ) x 2 = 4 ( giờ )
Quãng đường A - B là:
30 x 4 = 120 ( km )
Đáp số: 120 km
đúng cái nhé

Lời giải:
Vận tốc trung bình đi từ A đến B là:
$\frac{20+30}{2}=25$ (km/h)
Kiến thức cần nhớ:
Vận tốc trung bình bằng tổng quãng đường chia cho tổng thời gian đi hết quãng đường đó!
Công thức Vtb = \(\dfrac{S_1+S_2+...+S_n}{t_1+t_2+...+t_n}\)
Giải chi tiết:
Gọi quãng đường AB là: S (km); S > 0
Thời gian người đó đi hết nửa quãng đường đầu là:
\(\dfrac{S}{2}\) : 20 = \(\dfrac{S}{40}\) (giờ)
Thời gian người đó đi hết nửa quãng đường sau là:
\(\dfrac{S}{2}\) : 30 = \(\dfrac{S}{60}\) (giờ)
Vận tốc trung bình của người đó đi từ A đến B là:
Áp dụng công thức Vtb = \(\dfrac{S_1+S_2}{t_1+t_2}\) ta có
Vtb = \(\dfrac{S}{\dfrac{S}{40}+\dfrac{S}{60}}\)
Vtb = \(\dfrac{S}{S.\left(\dfrac{1}{40}+\dfrac{1}{60}\right)}\)
Vtb = \(\dfrac{1}{\dfrac{1}{24}}\)
Vtb = 24 (km/h)

Vận tốc trung bình của người đó trên toàn bộ quãng đường AB là:
(15 + 30) : 2 = 22,5 (km/h)
Đáp số: 22,5 km/h

Gọi vận tốc trung bình của người đó là: x(km/h)
Gọi độ dài nửa quãng đường AB là: a(km)
Khi đó ta có:
+ Thời gian đi nửa quãng đường đầu là: a/20(h)
+ Thời gian đi nửa quãng đường sau là: a/30(h)
→ Thời gian đi cả quãng đường AB là:
Do đó ta có: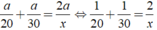
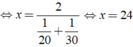
Vậy vận tốc cần tìm là 24km/h
Chọn đáp án B.

Gọi vận tốc trung bình của người đó là: x(km/h) (x > 0)
Gọi độ dài nửa quãng đường AB là: a(km)
Khi đó ta có:
+ Thời gian đi nửa quãng đường đầu là: a/20(h)
+ Thời gian đi nửa quãng đường sau là: a/30(h)
→ Thời gian đi cả quãng đường AB là:
Do đó ta có: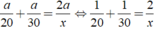
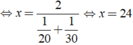
Vậy vận tốc cần tìm là 24km/h
Chọn đáp án B.

Bài 3:
\(x^4-x^3+x-1=0\)
\(\Rightarrow x^3\left(x-1\right)+\left(x-1\right)=0\)
\(\Rightarrow\left(x^3+1\right)\left(x-1\right)=0\)
\(\Rightarrow\left[\begin{matrix}x^3+1=0\\x-1=0\end{matrix}\right.\Rightarrow\left[\begin{matrix}x^3=-1\\x=1\end{matrix}\right.\Rightarrow\left[\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
Vậy \(x\in\left\{1;-1\right\}\)
Bài cuối:
Tóm tắt:
...
Giải
Lập phương trình:
Gọi thời điểm hai xe gặp nhau là x: x(giờ)
-Thời gian xe máy đi là: (x-8) (h)
-Thời gian oto là (x-8-24/60)(h)
ÁP dụng công thức S=vt ta có phương trình cân bằng quãng đường:
\(35.\left(x-8\right)+45\left(x-8-\dfrac{6}{15}\right)=90\)
Giải phương trình:
\(\Leftrightarrow\left(35+45\right)x=\left(90+35.8+45.8+\dfrac{45.6}{15}\right)=90+80.8+3.6\)
\(x=\dfrac{90+80.8+18}{80}=8+1+\dfrac{28}{80}=9+\dfrac{21}{60}\)(h)
Vậy: hai xe gặp lúc 9 giờ 21 phút
Câu 1:
Áp dụng BĐT Cô si cho 4 số dương, ta có:
\(a^4+b^4+c^4+d^4\ge4.^4\sqrt{\left(abcd\right)^4}=4abcd\)
Dấu "=" \(\Leftrightarrow a=b=c=d\)
Câu 2:
Gọi quãng đường AB là x km (x>0)
\(V_{tb}=\dfrac{S}{t}=\dfrac{x}{\dfrac{x}{\dfrac{2}{20}}+\dfrac{x}{\dfrac{2}{30}}}=\dfrac{x}{\dfrac{x}{40}+\dfrac{x}{60}}=\dfrac{x}{\dfrac{5x}{120}}=\dfrac{120x}{5x}=\dfrac{120}{5}=24\left(\text{km/h}\right)\)
Vậy ...
cảm ơn ạ :D