Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

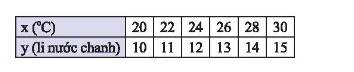
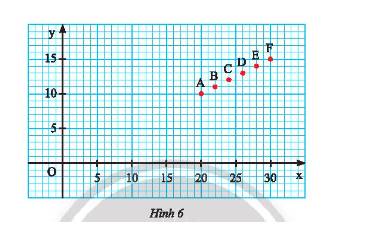
a) Điểm \(A\left( {20;10} \right);B\left( {22;11} \right);C\left( {24;12} \right);D\left( {26;13} \right);E\left( {28;14} \right);D\left( {30;15} \right)\)
Ta thấy mỗi cặp giá trị \(x;y\) tương ứng trong bảng là tọa độ của các điểm \(A;B;C;D;E;F\).

a) Ta có $f(-4)=\frac{4}{-4}=-1$; $f(8)=\frac{4}{8}=\frac{1}{2}$.
b)
x | -2 | -1 | 2 | 3 | $\frac{1}{2}$ |
y = f(x) | -2 | -4 | 2 | $\frac{4}{3}$ | 8 |

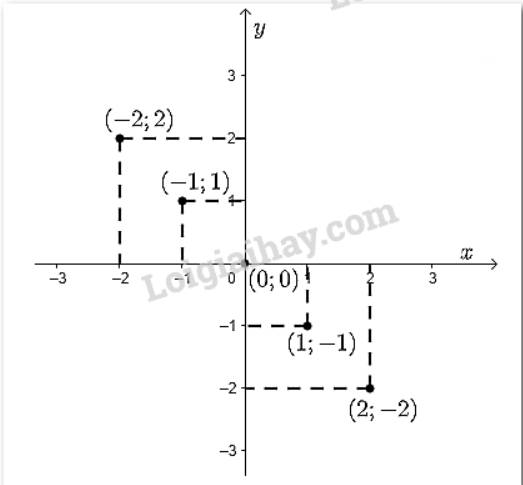
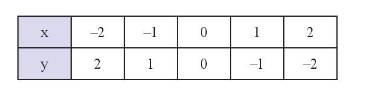
Đồ thị hàm số là tập hợp các điểm có tọa độ \(\left( { - 2;2} \right);\left( { - 1;1} \right);\left( {0;0} \right);\left( {1; - 1} \right);\left( {2; - 2} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây:

a) Dùng 
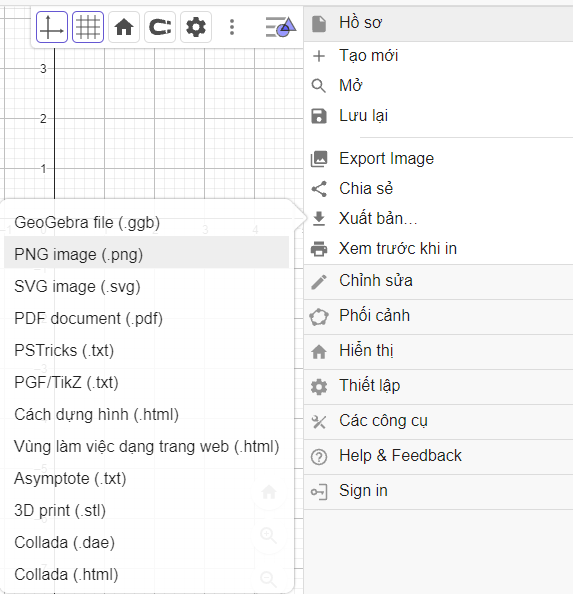
Vào Hồ sơ → Chọn Xuất bản → Chọn PNG image (.png).
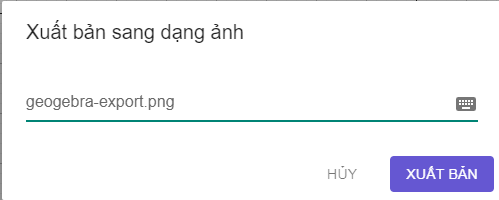
Ta đổi tên tệp thành hbh (như hình vẽ), sau đó chọn xuất bản.
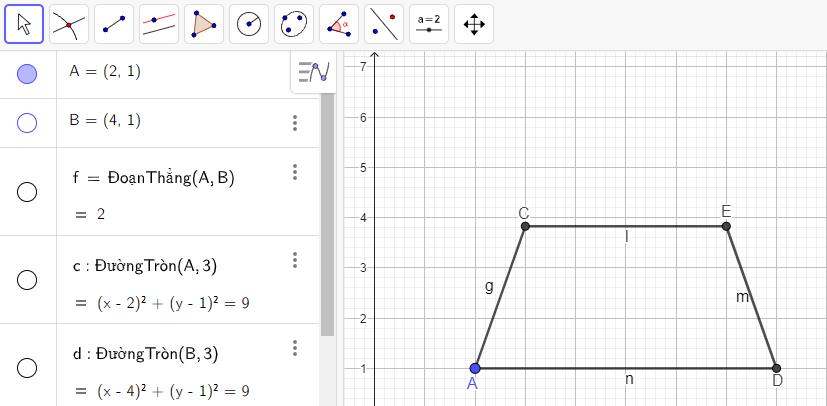
c) Vẽ hình thang cân ADEC có AD // EC, AD = 6 cm, CE = 4 cm, AC = DE = 3 cm theo các bước sau:
Bước 1. Vẽ đoạn thẳng AB và có độ dài bằng AD – EC = 2 cm tương tự như Bước 1 của HĐ1.
Bước 2. Vẽ tam giác ABC có BC = 3 cm (độ dài của DE), AC = 3 cm.
Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

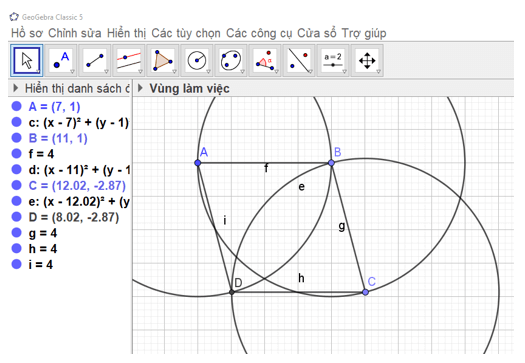
Bước 4. Vẽ điểm E sao cho DE // BC và CE // AB.
Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Ẩn các đường tròn, các đường thẳng, đoạn thẳng AB, BC và điểm B. Chọn công cụ 

a) Dùng 

b) Lưu hình vẽ ở HĐ2 thành tệp hbh.png.
Vào Hồ sơ → Chọn Xuất bản → Chọn PNG image (.png).
Ta đổi tên tệp thành hbh (như hình vẽ), sau đó chọn xuất bản.
Bước 1. Vẽ đoạn thẳng AB và có độ dài 4 cm tương tự như Bước 1 của HĐ1.
Bước 2. Vẽ điểm C sao cho BC = 4 cm.
Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 
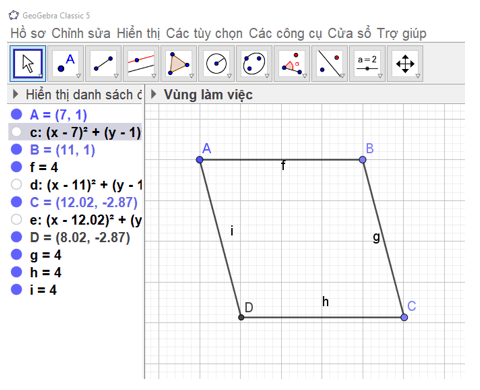
Bước 3. Ẩn đường tròn và thu được hình thoi ABCD.

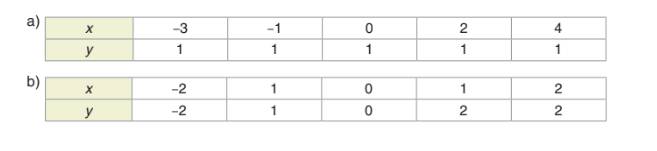
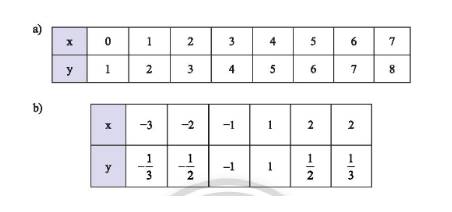
a) Bảng a đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ nhận được duy nhất một giá trị tương ứng của \(y\).
b) Bảng b đại lượng \(y\) không là hàm số của đại lượng \(x\) vì có những giá trị của \(x\) cho ta hai giá trị \(y\).
Với \(x = 2\) cho ta hai giá trị \(y\) là \(y = \dfrac{1}{2}\) và \(y = \dfrac{1}{3}\).

Đại lượng y là hàm số của đại lượng x. Bởi vì với mỗi giá trị của x chỉ tìm được duy nhất một giá trị tương ứng của y

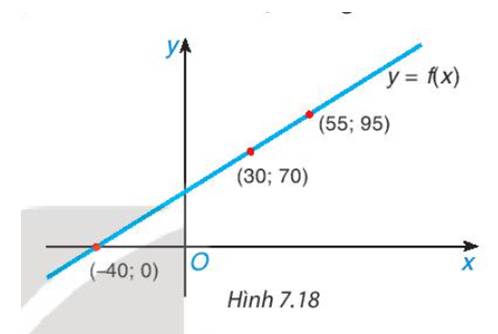
a) f(x) = 70 ⇒ x = 30
b) f(x) = 95 ⇒ x = 55
c) f(x) = 0 ⇒ x = −40



 trong công cụ
trong công cụ  để kiểm tra DE có bằng 4 cm không.
để kiểm tra DE có bằng 4 cm không.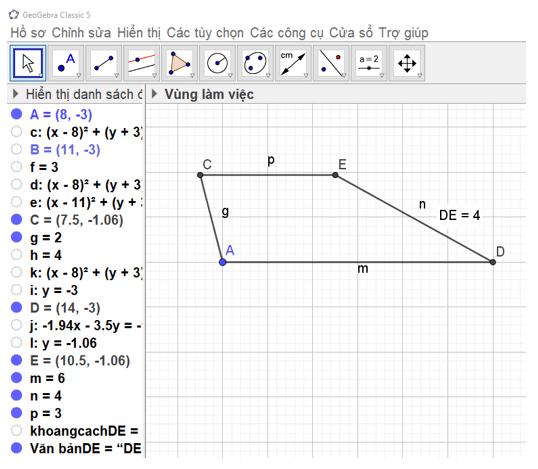
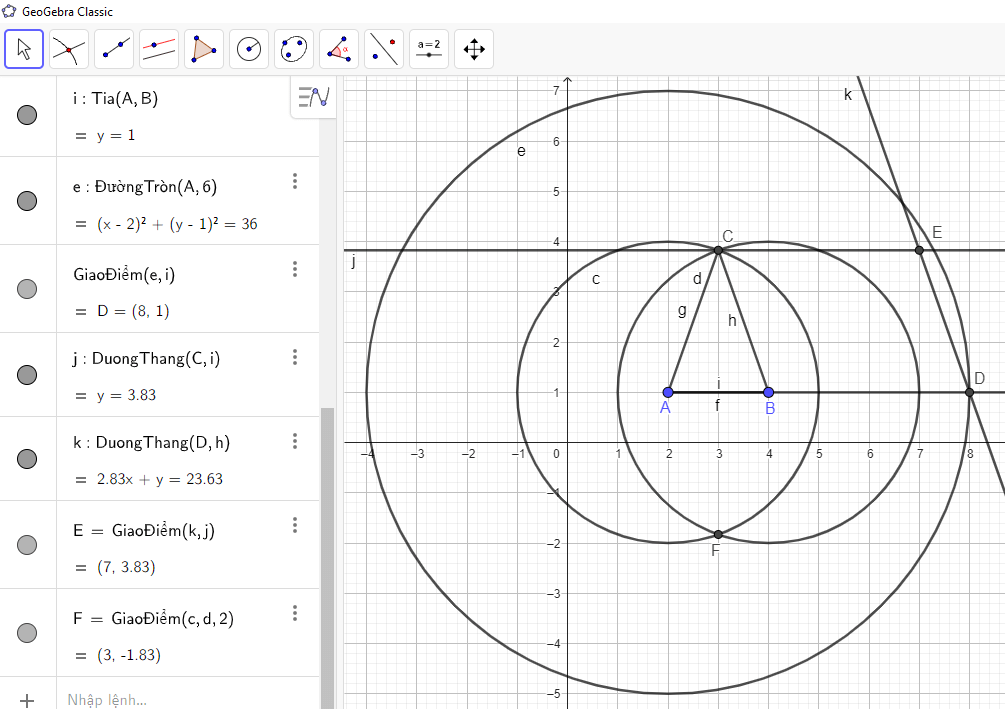
 trong công cụ
trong công cụ  để kiểm tra trung điểm AC và BD có trùng nhau không.
để kiểm tra trung điểm AC và BD có trùng nhau không.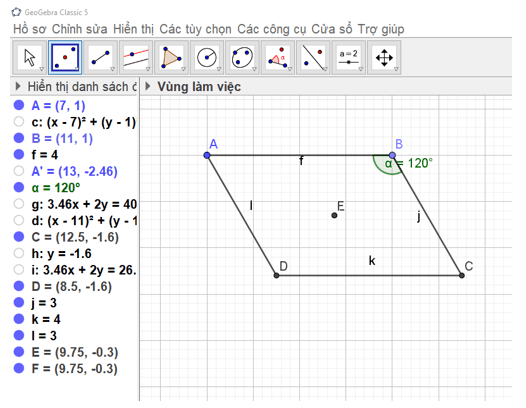
a) Đại lượng y là hàm số của x vì với mỗi giá trị của x (thuộc tập hợp {-3; -1; 0; 2; 4}) ta luôn xác định được chỉ một giá trị tương ứng của y (y luôn bằng 1).
b) Đại lượng y không là hàm số của x vì với x = 1 ta xác định được hai giá trị tương ứng của y là y = 1 và y = 2.