Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đại lượng y là hàm số của đại lượng x bởi vì với mỗi giá trị của x, chỉ nhận được duy nhất 1 giá trị của đại lượng y

a) Đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ xác nhận được duy nhất một giá trị \(y\) tương ứng.
b) \(f\left( 2 \right) = {2^2} = 4;f\left( { - 3} \right) = {\left( { - 3} \right)^2} = 9\)
Ta có: \(f\left( { - 2} \right) = {\left( { - 2} \right)^2} = 4;f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)
\(f\left( 0 \right) = {0^2} = 0;f\left( 1 \right) = {1^2} = 1\)
\(f\left( 2 \right) = {2^2} = 4;f\left( 3 \right) = {3^2} = 9\)
\(x\) | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
\(f\left( x \right)\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |

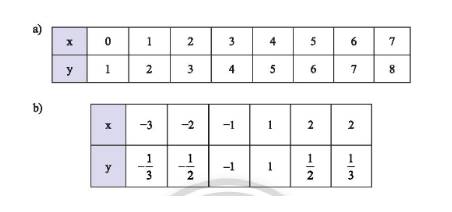
a) Bảng a đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ nhận được duy nhất một giá trị tương ứng của \(y\).
b) Bảng b đại lượng \(y\) không là hàm số của đại lượng \(x\) vì có những giá trị của \(x\) cho ta hai giá trị \(y\).
Với \(x = 2\) cho ta hai giá trị \(y\) là \(y = \dfrac{1}{2}\) và \(y = \dfrac{1}{3}\).

Với \(x = 4\) ta được. \(y = 2.4 + 3 = 11\)
Với \(x = 6\) ta được. \(y = 2.6 + 3 = 15\)
\(x\) | 1 | 2 | 3 | 4 | 6 |
\(y = 2x + 3\) | 5 | 7 | 9 | 11 | 15 |

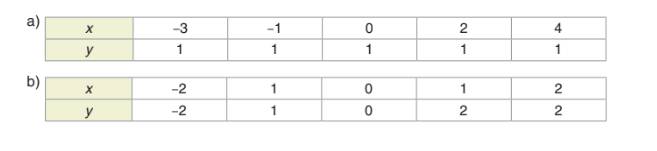
a) Đại lượng y là hàm số của x vì với mỗi giá trị của x (thuộc tập hợp {-3; -1; 0; 2; 4}) ta luôn xác định được chỉ một giá trị tương ứng của y (y luôn bằng 1).
b) Đại lượng y không là hàm số của x vì với x = 1 ta xác định được hai giá trị tương ứng của y là y = 1 và y = 2.

a) Quan sát bảng trên ta thấy khi x = 1; x = 2; x = 3; x = 4; x = 5; x = 6 thì ta đều xác định giá trị của y là y = − 2.
Vì với mỗi giá trị của x ta xác định được một giá trị của y nên đại lượng y là hàm số của đại lượng x.
b) Quan sát bảng trên ta thấy khi x = 1; x = 2; x = 3; x = 4; x = 1; x = 5 thì ta đều xác định giá trị của y lần lượt là: y = − 2; y = − 3; y = − 4; y = − 5; y = − 6; y = − 7.
Vì x = 1 nhận hai giá trị y = -2 và y = -6 nên đại lượng y không là hàm số của đại lượng x.

câu 1:\(3^{30}=3^{3^{10}}=27^{10};5^{20}=5^{2^{10}}=25^{10}\)do 27>25 nên \(27^{10}>25^{10}\)hay \(3^{30}>5^{20}\)
câu 2: mình tạm chỉnh lại đề tý
\(\hept{\begin{cases}x^2=zy\left(1\right)\\y^2=xz\left(2\right)\\z^2=xy\left(3\right)\end{cases}}\)lấy (1) chia (2) và (2) chia (3) ta được\(\hept{\begin{cases}\frac{x^2}{y^2}=\frac{y}{x}\\\frac{y^2}{z^2}=\frac{z}{y}\end{cases}\Rightarrow\hept{\begin{cases}y^3=x^3\\y^3=z^3\end{cases}}\Rightarrow x^3=y^3=z^3\Rightarrow x=y=z}\)
câu 3:
\(\frac{x-1}{2009}-1+\frac{x-2}{2008}-1=\frac{x-3}{2007}-1+\frac{x-4}{2006}-1\)
\(\frac{x-2010}{2009}+\frac{x-2010}{2008}=\frac{x-2010}{2007}+\frac{x-2010}{2006}\)
\(\left(x-2010\right).\left(\frac{1}{2009}+\frac{1}{2008}\right)=\left(x-2010\right).\left(\frac{1}{2007}+\frac{1}{2006}\right)\)
Do đó để 2 vế bằng nhau thì x-2010=0=>x=2010
câu 4: vì x và y là hai đại lượng tỉ lệ nghịch nên ta có Công thức \(x.y=x_1.y_1=x_2.y_2=k\Leftrightarrow2.y_1=3.y_2\Rightarrow y_1=\frac{3}{2}y_2\)
thay \(y_1=\frac{3}{2}y_2\)vào phương trình \(y^2_1+y^2_2=52\)
\(\frac{9}{4}y_2^2+y_2^2=52\Rightarrow\frac{13}{4}y_2^2=52\Rightarrow\hept{\begin{cases}y_2=4\\y_2=-4\end{cases}}\Rightarrow\hept{\begin{cases}y_1=6\\y_1=-6\end{cases}}\)


Đại lượng y là hàm số của đại lượng x. Bởi vì với mỗi giá trị của x chỉ tìm được duy nhất một giá trị tương ứng của y