Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

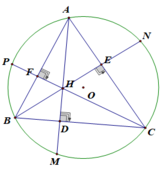
d) Tam giác ADB vuông tại D có: ∠(A1) + ∠(ABC) = 90o (1)
Tam giác BCF vuông tại F có: ∠(C1) + ∠(ABC) = 90o (2)
Từ (1)và (2) ⇒ ∠(A1) = ∠(C1)
Mặt khác, ta có: ∠( A 1 ) = ∠( C 2 ) ( 2 góc nội tiếp cùng chắn cung BM)
⇒ ∠( C 1 ) = ∠( C 2 )
⇒ CD là tia phân giác của góc HCM
Xét tam giác HCM có: CD vừa là tia phân giác vừa là đường cao (CD⊥HD)
⇒ Δ HCM cân tại C
⇒ CD cũng là trung tuyến của của HM hay H và M đối xứng với nhau qua D.

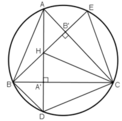
a) Xét tứ giác BNHM có
\(\widehat{BNH}\) và \(\widehat{BMH}\) là hai góc đối
\(\widehat{BNH}+\widehat{BMH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BNHM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Từ tam giác cân BHD suy ra HA'=A'D (BA' là đường trung trực của cạnh HD)
Điểm C nằm trên đường trung trực của HD nên CH=CD.

* Cách 1.
Ta có: AD vuông BC tại A' nên A A ' B ^ = 90 o
Vì A A ' B ^ là góc có đỉnh bên trong đường tròn nên:
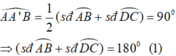
Tương tự, vì BE vuông góc AC tại B' nên ta có:
E B ' C ^ là góc có đỉnh nằm trong đường tròn
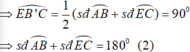
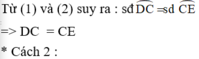
Ta có:![]() (1)
(1)
Và ![]() (2)
(2)
Tà (1) và (2) ![]()
Đây là hai góc nội tiếp chắc hai cung DC và CE nên:
![]()
a, Xét từ giác AMNB ta có:
BM | AC => góc AMB =90
AN | BC => góc ANB =90
=> AMB = ANB
Mà: điểm M và N cùng nhìn 1 cạnh AB
=> AMNB nội tiếp => góc ABM = góc MBN
Hay: sđ cung EC =sđ cung DC
=> đpcm
b, Xét tứ giác MCNH , ta có:
góc HMC =90 và góc HNC =90
=> góc HMC + góc HNC =180
=> Tứ giác MCNH nội tiếp => góc HMN = góc HCN
Mà: góc HMN= góc NAB (cùng chắn cung BN)
Hay gócNAB = góc BCD (cùng chắn cung BD)
Từ trên suy ra: góc HCN = góc NCD
Xét 2 tam giác: tg HCN và tg NCD
góc HNC= góc CND = 90
NC chung
góc HCN = góc NCD
=> tg HCN = tg NCD (gcg)
=> HN=ND =>đpcm