Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a) \(A=\sqrt{8}+\sqrt{18}-\sqrt{32}\)
\(=2\sqrt{2}+3\sqrt{2}-4\sqrt{2}\)
\(=\sqrt{2}\)
b) \(B=\sqrt{9-4\sqrt{5}}-\sqrt{5}\)
\(=\sqrt{4-4\sqrt{5}+5}-\sqrt{5}\)
\(=\sqrt{\left(2-\sqrt{5}\right)^2}-\sqrt{5}\)
\(=\left|2-\sqrt{5}\right|-\sqrt{5}\)
\(=\sqrt{5}-2-\sqrt{5}\)
\(=-2\)
Bài 2:
a) \(\left\{{}\begin{matrix}2x-3y=4\\x+3y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x=6\\x+3y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\2+3y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
Vậy phương trình có nghiệm là: \(\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
b) ĐKXĐ: \(x\ne\pm2\)
Với \(x\ne\pm2\), ta có:
\(\dfrac{10}{x^2-4}+\dfrac{1}{2-x}=1\)
\(\Leftrightarrow\dfrac{10}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x-2}=1\)
\(\Leftrightarrow\dfrac{10-x-2}{x^2-4}=1\)
\(\Leftrightarrow\dfrac{8-x}{x^2-4}=1\)
\(\Rightarrow x^2-4=8-x\)
\(\Leftrightarrow x^2+x-12=0\)
\(\Leftrightarrow x^2-3x+4x-12=0\)
\(\Leftrightarrow x\left(x-3\right)+4\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+4=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-4\end{matrix}\right.\) (TM)
Vậy phương trình có tập nghiệm là: S ={3; -4}

\(P=\left(a+1\right)\left(a^2+1\right)\left(a^4+1\right)...\left(a^{32}+1\right)\left(a^{64}+1\right)\)
\(\Leftrightarrow10P=\left(a-1\right)\left(a+1\right)\left(a^2+1\right)...\left(a^{64}+1\right)\)
\(\Leftrightarrow10P=\left(a^2-1\right)\left(a^2+1\right)\left(a^4+1\right)...\left(a^{64}+1\right)\)
\(\Leftrightarrow10P=\left(a^4-1\right)\left(a^4+1\right)...\left(a^{64}+1\right)\)
Tiếp tục rút gọn, ta được : \(10P=a^{128}-1\Leftrightarrow P=\frac{a^{128}-1}{10}=\frac{11^{128}-1}{10}\)

Phương trình 9 x 2 +6x+1 =0 có hệ số a=9,b’=3,c=1
Ta có: ∆ ’ = b ' 2 – ac = 3 2 -9.1 = 9 - 9 = 0
Phương trình có nghiệm kép:
x 1 = x 2 = -b'/a =-3/9 =-1/3

2 công nhân làm cùng cv trong 4 ngày
\(\rightarrow\)1 ngày làm 1/4 công việc
người thứ 1 làm mất 6 ngày
\(\rightarrow\)1 ngày làm 1/6 công việc
gọi a là số công việc người 2 lm trong 1 ngày
ta có pt \(\frac{1}{4}=\frac{1}{6}+a\)---> \(a=\frac{1}{12}\)
----> người 2 lm hết cv trong 12 ngày
mình ko hiểu câu hỏi b cko lắm

a) \(\sqrt[]{x-9}+2\sqrt[]{y-2}+3\sqrt[]{z-3}=\dfrac{x+y+z}{2}\left(1\right)\)
\(Đkxđ:\left\{{}\begin{matrix}x\ge9\\y\ge2\\z\ge3\end{matrix}\right.\)
Áp dụng Bất đẳng thức Bunhiacopxki :
\(\left(1\sqrt[]{x-9}+2\sqrt[]{y-2}+3\sqrt[]{z-3}\right)^2\le\left(1^2+2^2+3^2\right)\left(x-9+y-2+z-3\right)=14\left(x+y+z-14\right)\)
Dấu "=" xảy ra khi và chỉ khi :
\(\dfrac{x-9}{1}=\dfrac{y-2}{2}=\dfrac{z-3}{3}\left(a\right)\)
\(\left(1\right)\Leftrightarrow\)\(14\left(x+y+z-14\right)=\dfrac{\left(x+y+z\right)^2}{4}\left(2\right)\)
Đặt \(t=x+y+z\)
\(\Leftrightarrow14t-196=\dfrac{t^2}{4}\)
\(\Leftrightarrow t^2+56t-784=0\)
\(\Leftrightarrow\left(t-28\right)^2=0\)
\(\Leftrightarrow t=28\)
\(\Leftrightarrow x+y+z=28\)
\(\left(a\right)\Leftrightarrow\dfrac{x-9}{1}=\dfrac{y-2}{2}=\dfrac{z-3}{3}=\dfrac{x+y+z-14}{6}=\dfrac{28-14}{6}=\dfrac{7}{3}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-9=1.\dfrac{7}{3}=\dfrac{7}{3}\\y-2=2.\dfrac{7}{3}=\dfrac{14}{3}\\z-3=3.\dfrac{7}{3}=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{34}{3}\\y=\dfrac{20}{3}\\z=10\end{matrix}\right.\)

Bài 6 :
Xét tam giác vuông AHC tại H có :
\(AC^2=AH^2+CH^2=144+25=169\)
\(\Rightarrow AC=13\left(cm\right)\)
\(sinC=\dfrac{AH}{AC}=\dfrac{12}{13}\)
\(sin^2C+cos^2C=1\Rightarrow cos^2C=1-sin^2C\)
\(\Rightarrow cos^2C=1-\dfrac{144}{169}=\dfrac{25}{169}\)
\(\Rightarrow cosC=\dfrac{5}{13}\left(cos>0\right)\)
\(sinB=sin\left(90^o-C\right)=cosC=\dfrac{5}{13}\)
Bài 7 :
Ta có :
\(\widehat{B}+\widehat{C}=90^o\) (tam ABC vuông tại A)
\(\Leftrightarrow\widehat{C}=90^o-\widehat{B}=90^o-45^o=45^o\)
\(\Rightarrow\left\{{}\begin{matrix}sin\widehat{C}=sin45^o=\dfrac{\sqrt[]{2}}{2}\\cos\widehat{C}=cos45^o=\dfrac{\sqrt[]{2}}{2}\\tan\widehat{C}=tan45^o=1\\cot\widehat{C}=cot45^o=1\end{matrix}\right.\)

1.\(A=\left(\sqrt{3}+1\right)\sqrt{\dfrac{14-6\sqrt{3}}{5+\sqrt{3}}}=\left(\sqrt{3}+1\right)\sqrt{\dfrac{\left(14-6\sqrt{3}\right)\left(5-\sqrt{3}\right)}{\left(5+\sqrt{3}\right)\left(5-\sqrt{3}\right)}}\)
\(=\left(\sqrt{3}+1\right)\sqrt{\dfrac{44\left(2-\sqrt{3}\right)}{22}}=\left(\sqrt{3}+1\right)\sqrt{4-2\sqrt{3}}=\left(\sqrt{3}+1\right)\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(=\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)=2\)
2.1.a) \(x^2=\left(x-1\right)\left(3x-2\right)\Leftrightarrow x^2=3x^2-5x+2\Leftrightarrow2x^2-5x+2=0\)
\(\Leftrightarrow\left(x-2\right)\left(2x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{2}\end{matrix}\right.\)
b) \(9x^4+5x^2-4=0\Leftrightarrow9x^4+9x^2-4x^2-4=0\)
\(\Leftrightarrow9x^2\left(x^2+1\right)-4\left(x^2+1\right)=0\Leftrightarrow\left(x^2+1\right)\left(9x^2-4\right)=0\)
mà \(x^2+1>0\Rightarrow9x^2=4\Rightarrow x^2=\dfrac{4}{9}\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
2) Gọi số xe lúc đầu của đội là a(xe) \(\left(a\in N,a>0\right)\)
Theo đề,ta có: \(\left(a-2\right)\left(\dfrac{120}{a}+3\right)=120\Leftrightarrow120+3a-\dfrac{240}{a}-6=120\)
\(\Leftrightarrow\dfrac{3a^2-6a-240}{a}=0\Rightarrow3a^2-6a-240=0\Rightarrow a^2-2a-80=0\)
\(\Leftrightarrow\left(a+8\right)\left(a-10\right)=0\) mà \(a>0\Rightarrow a=10\)

b; \(\text{Δ}=1^2-4\cdot\left(-2\right)\cdot\left(-3\right)=1-4\cdot6=-23< 0\)
Do đó: Phương trình vô nghiệm
c: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot11=1+44=45>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{1-3\sqrt{5}}{-2}=\dfrac{3\sqrt{5}-1}{2}\\x_2=\dfrac{-3\sqrt{5}-1}{2}\end{matrix}\right.\)
a, \(\Delta'=2-\left(-6\right)=8>0\)
vậy pt luôn có 2 nghiệm pb
\(x_1=-\sqrt{2}-2\sqrt{2};x_2=-\sqrt{2}+2\sqrt{2}\)
b, \(\Delta=1-4\left(-3\right)\left(-2\right)=1-16< 0\)
pt vô nghiệm
c, \(\Delta=1-4.11\left(-1\right)=1+44=45>0\)
pt luôn có 2 nghiệm pb
\(x_1=\dfrac{-1-3\sqrt{5}}{-2};x_2=\dfrac{-1+3\sqrt{5}}{-2}\)

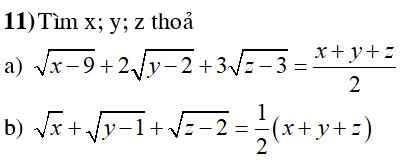

xin cái link lời giải với , t rất cần