
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1)
a) 4y2-4xy+x2= x2-4xy+4y2= (x-2y)2
b) 9x2-12xy+4y2= (3x)2-2.3x.2y+(2y)2= (3x-2y)2
c) 16x2-25=(4x)2-52= (4x-5)(4x+5)
d) 1-9y2= 12-(3y)2=(1-3y)(1+3y)
g) x3-27y3= (x-3y)(x2+3xy+9y2)
h) 64 + 8x3=(4+2x)(16+8x+4x2)

a) \(\left(4x^{^5}-8x^3\right):\left(-2x^3\right)\)
\(=\left(2x^{10}-2x^9\right):\left(-2x^3\right)\)
\(=\left[2x^{10}:\left(-2x^3\right)\right]-\left[2x^9:\left(-2x^3\right)\right]\)
\(=-x^7+x^6\)
Bài 2:
\(a,=-2x^2+4\\ b,=-3x^2+4x-1\\ c,=-\dfrac{1}{2}-2xy+\dfrac{3}{2}x^2y^2\\ d,=6-8xy+2x^2y^2\\ e,=2\left(x-y\right)^2-7\left(x-y\right)+1\\ f,=\dfrac{3}{5}\left(x-y\right)^3-\dfrac{2}{5}\left(x-y\right)^2+\dfrac{3}{5}\)

Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)

4A:
a: \(A=3xy-2x+4x^2y^2\)
\(=3\cdot\left(-1\right)\cdot2-2\cdot\left(-1\right)+4\cdot\left(-1\right)^2\cdot2^2\)
\(=-6+2+16\)
=12

Bài 1:
a: \(=15x^2-6x+5x-2\)
\(=\left(5x-2\right)\left(3x+1\right)\)
b: \(=4x^2-8x-x+2\)
\(=\left(x-2\right)\left(4x-1\right)\)

Δ ABC ∼ Δ A'B'C' theo tỉ số đồng dạng \(\dfrac{1}{2}\) nên ta có:
\(\dfrac{AB}{A'B'}\)=\(\dfrac{BC}{B'C'}\)=\(\dfrac{AC}{A'C'}\)=\(\dfrac{1}{2}\)
=>\(\dfrac{AB}{A'B'}\)=\(\dfrac{BC}{B'C'}\)=\(\dfrac{AC}{A'C'}\) =\(\dfrac{AB+BC+AC}{A'B'+B'C'+A'C'}\)= \(\dfrac{1}{2}\)
Vậy Δ ABC ∼ Δ A'B'C' theo tỉ số đồng dạng là \(\dfrac{1}{2}\)

2:
a: ĐKXĐ: \(x\notin\left\{0;-4\right\}\)
\(\dfrac{6}{x^2+4x}+\dfrac{3}{2x+8}\)
\(=\dfrac{6}{x\left(x+4\right)}+\dfrac{3}{2\left(x+4\right)}\)
\(=\dfrac{12+3x}{2x\left(x+4\right)}=\dfrac{3\left(x+4\right)}{2x\left(x+4\right)}=\dfrac{3}{2x}\)
b: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{x+1}{x-2}+\dfrac{x-2}{x+2}+\dfrac{x-14}{x^2-4}\)
\(=\dfrac{\left(x+1\right)\cdot\left(x+2\right)+\left(x-2\right)^2+x-14}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+3x+2+x^2-4x+4+x-14}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x^2-8}{x^2-4}=2\)
c: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
\(\dfrac{2}{x+1}+\dfrac{-4}{1-x}+\dfrac{5x+1}{1-x^2}\)
\(=\dfrac{2}{x+1}+\dfrac{4}{x-1}-\dfrac{5x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{2x-2+4x+4-5x-1}{\left(x+1\right)\left(x-1\right)}=\dfrac{x+1}{\left(x+1\right)\left(x-1\right)}=\dfrac{1}{x-1}\)
d: ĐKXĐ: \(x\ne\pm y\)
\(\dfrac{x}{x^2+xy}+\dfrac{x-3y}{y^2-x^2}+\dfrac{x}{xy-x^2}\)
\(=\dfrac{x}{x\left(x+y\right)}-\dfrac{x-3y}{\left(x-y\right)\left(x+y\right)}-\dfrac{x}{x\left(x-y\right)}\)
\(=\dfrac{1}{x+y}-\dfrac{x-3y}{\left(x-y\right)\left(x+y\right)}-\dfrac{1}{x-y}\)
\(=\dfrac{x-y-x+3y-x-y}{\left(x-y\right)\left(x+y\right)}=\dfrac{-x+y}{\left(x-y\right)\left(x+y\right)}=\dfrac{-1}{x+y}\)
e: ĐKXĐ: \(\left\{{}\begin{matrix}x< >0\\y< >0;x\ne y\end{matrix}\right.\)
\(\dfrac{y}{x^2-xy}+\dfrac{x}{y^2-xy}\)
\(=\dfrac{y}{x\left(x-y\right)}-\dfrac{x}{y\left(x-y\right)}\)
\(=\dfrac{y^2-x^2}{xy\left(x-y\right)}=\dfrac{-\left(x-y\right)\left(x+y\right)}{xy\left(x-y\right)}=\dfrac{-x-y}{xy}\)
f: ĐKXĐ: x<>1
\(\dfrac{11x-4}{x-1}+\dfrac{10x+4}{2-2x}\)
\(=\dfrac{11x-4}{x-1}-\dfrac{5x+2}{x-1}\)
\(=\dfrac{11x-4-5x-2}{x-1}=\dfrac{6x-6}{x-1}=6\)

Bài 5:
e: \(\dfrac{2}{x+1}=\dfrac{2x^2-2x+2}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(\dfrac{3}{x^2-x+1}=\dfrac{3x+3}{\left(x+1\right)\left(x^2-x+1\right)}\)
 bài 2 thôi ạ
bài 2 thôi ạ  Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!
Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!


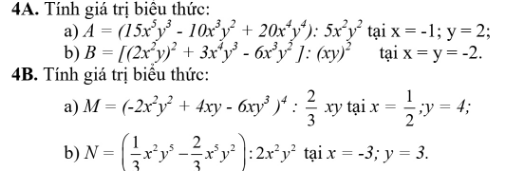
 giúp em bài 3 thôi ạ
giúp em bài 3 thôi ạ 

