
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có (x+1)^3 - (x-1)^3
=(x3+3x2+3x+1)-(x3-3x2+3x-1)
= x3 + 3x2 +3x +1 - x3 + 3x2 -3x + 1
=6x2 + 2
Vậy biểu thức này có phụ thuộc vào biến x (vì vẫn còn 6x2)
Chúc bạn học tốt!

a) \(x^2+xy+x\)
\(=x\left(x+y+1\right)\)
Thay x=77, y=22
\(=77\left(77+22+1\right)\)
\(=77.100=7700\)
b) \(x\left(x-y\right)+y\left(y-x\right)\)
\(=\left(x-y\right)\left(x-y\right)\)
\(=\left(x-y\right)^2\)
Thay x=53, y=3
\(=\left(53-3\right)^2\)
\(=50^2=2500\)
c) \(x\left(x-1\right)-y\left(1-x\right)\)
\(=\left(x+y\right)\left(x-1\right)\)
Thay x=2021, y=2029
\(=\left(2021+2019\right)\left(2021-1\right)\)
\(=4040.2020\)
\(=8160800\)
Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ

a: Xét tứ giác ABQN có
\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)
=>ABQN là hình chữ nhật
b: Xét ΔCAD có
DN,CH là các đường cao
DN cắt CH tại M
Do đó: M là trực tâm của ΔCAD
=>AM\(\perp\)CD
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
=>\(HA=\sqrt{HB\cdot HC}\)

Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)

\(2,\\ a,=2x^2+4x-3x-6-2x^2-4x-2=-3x-8\\ b,=\left[x-2+2\left(x+1\right)\right]^2=\left(x-2+2x+2\right)^2=9x^2\)

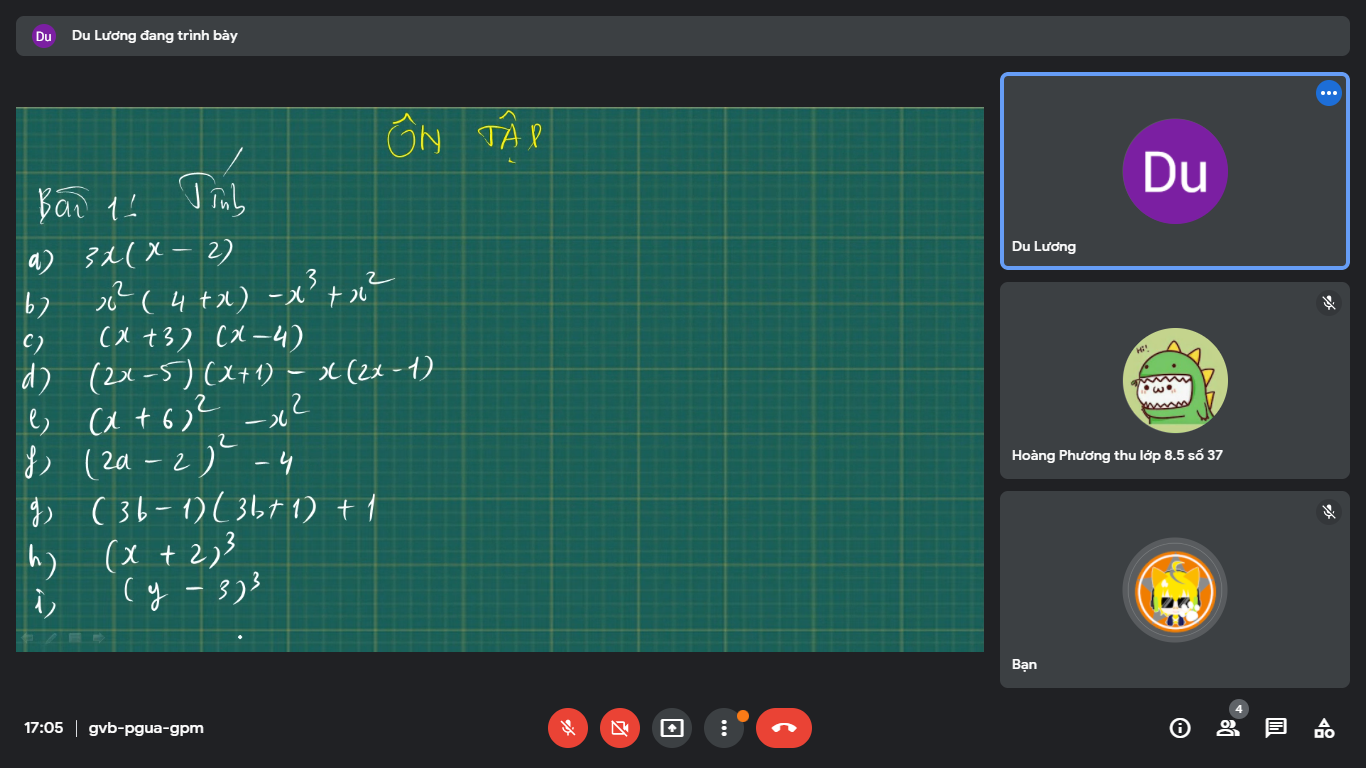
\(a,=3x^2-6x\\ b,=4x^2+x^3-x^3+x^2=5x^2\\ c,=x^2-4x+3x-12=x^2-x-12\\ d,=2x^2+2x-5x-5-2x^2+x=-2x-5\\ e,=x^2+12x+36-x^2=12x+36\\ f,=4a^2-8a+4-4=4a^2+8a\\ g,=9b^2-1+1=9b^2\\ h,=x^3+6x^2+12x+8\\ i,=y^3-9y^2+27y-27\)

b) Bạn đã chứng minh được tứ giác EKFC là hình bình hành ở câu a, mà EF cắt CK tại I \(\Rightarrow\)I là trung điểm EF (tính chất hình bình hành)
\(\Rightarrow AI\)là trung tuyến của \(\Delta AEF\)
Mà \(\Delta AEF\)vuông tại A \(\Rightarrow AI=\frac{1}{2}EF\)(tính chất tam giác vuông)
Lại có \(EI=\frac{1}{2}EF\)do I là trung điểm của đoạn EF \(\Rightarrow AI=EI\left(=\frac{1}{2}EF\right)\)
Mặt khác \(BE\perp AF\), \(MI\perp AF\left(gt\right)\)\(\Rightarrow BE//MI\)(quan hệ từ vuông góc đến song song)
Mà tứ giác BEFD là hình bình hành \(\Rightarrow BD//EF\)(tính chất hình bình hành)
\(\Rightarrow BM//EI\)(vì \(M\in BD;I\in EF\))
Xét tứ giác BEIM có \(BE//MI\left(cmt\right);BM//EI\left(cmt\right)\)\(\Rightarrow\)Tứ giác BEIM là hình bình hành (định nghĩa)
\(\Rightarrow BM=EI\)(tính chất hình bình hành)
Mà \(AI=EI\left(cmt\right)\)\(\Rightarrow AI=BM\left(=EI\right)\left(đpcm\right)\)
c) Do tứ giác BEFD là hình bình hành \(\Rightarrow\hept{\begin{cases}BE//DF\\BE=DF\end{cases}}\)(tính chất hình bình hành)
Mà \(\hept{\begin{cases}BE\perp CF\\BE=CF\end{cases}}\left(gt\right)\Rightarrow\hept{\begin{cases}DF\perp CFtạiF\\DF=CF\end{cases}}\)\(\Rightarrow\)F nằm trên đường trung trực của đoạn CD và \(\Delta CDF\)vuông cân tại F
\(\Rightarrow\widehat{DCF}=45^0\)
\(\Delta ABC\)vuông cân tại A (gt) \(\Rightarrow\widehat{ACB}=45^0\)
\(\Rightarrow\widehat{BCD}=180^0-\widehat{ACB}-\widehat{DCF}=180^0-45^0-45^0=90^0\)
\(\Rightarrow\Delta BCD\)vuông tại C.
Xét hình thang BEFD (BE//DF) ta có I là trung điểm EF (cmt) và IM//BE (cmt) \(\Rightarrow\)M là trung điểm của đoạn BD
\(\Rightarrow\)CM là trung tuyến của \(\Delta BCD\)
Mặt khác \(\Delta BCD\)vuông tại C \(\Rightarrow CM=\frac{1}{2}BD\)(tính chát tam giác vuông)
Mà \(DM=\frac{1}{2}BD\)do M là trung điểm BD \(\Rightarrow DM=CM\left(=\frac{1}{2}BD\right)\)
\(\Rightarrow\)M nằm trên đường trung trực của đoạn CD.
Mà F cũng nằm trên đường trung trực của đoạn CD (cmt)
\(\Rightarrow\)MF là đường trung trực của đoạn CD \(\Rightarrow\)C đối xứng với D qua MF (đpcm)



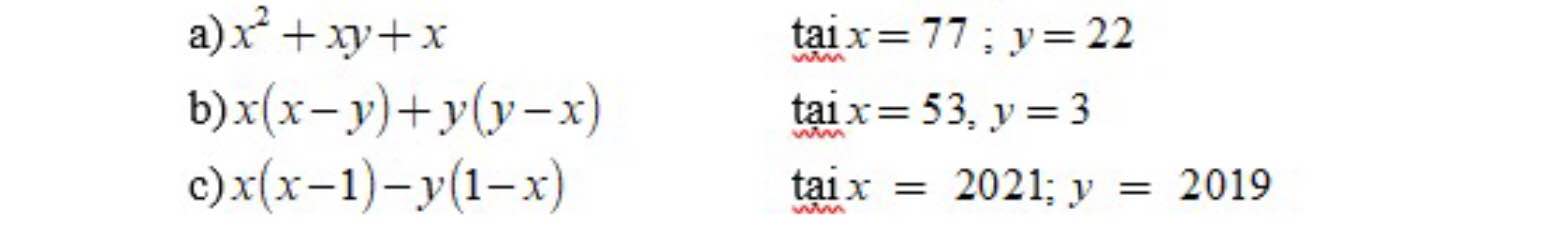 bài này nữa thôi các anh chị :3 em cảm ơn nhiều ạ
bài này nữa thôi các anh chị :3 em cảm ơn nhiều ạ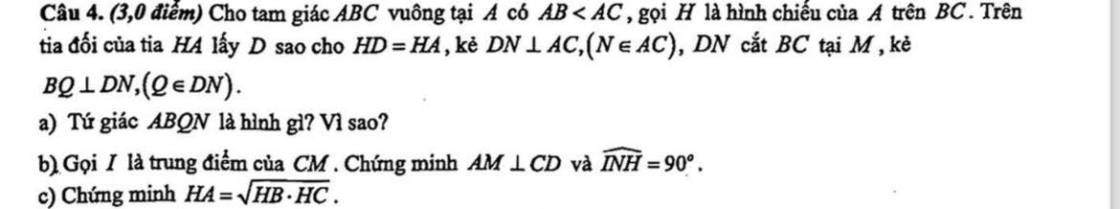


 mong mn giúp ạ.Cảm ơn mn.
mong mn giúp ạ.Cảm ơn mn. GIÚP MÌNH BÀI 4 CÂU B,C THÔI Ạ MÌNH CẢM ƠN NHIỀU
GIÚP MÌNH BÀI 4 CÂU B,C THÔI Ạ MÌNH CẢM ƠN NHIỀU Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!
Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!
Δ ABC ∼ Δ A'B'C' theo tỉ số đồng dạng \(\dfrac{1}{2}\) nên ta có:
\(\dfrac{AB}{A'B'}\)=\(\dfrac{BC}{B'C'}\)=\(\dfrac{AC}{A'C'}\)=\(\dfrac{1}{2}\)
=>\(\dfrac{AB}{A'B'}\)=\(\dfrac{BC}{B'C'}\)=\(\dfrac{AC}{A'C'}\) =\(\dfrac{AB+BC+AC}{A'B'+B'C'+A'C'}\)= \(\dfrac{1}{2}\)
Vậy Δ ABC ∼ Δ A'B'C' theo tỉ số đồng dạng là \(\dfrac{1}{2}\)