Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

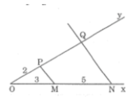
* Cách dựng:
- Dựng hai tia chung gốc ox và Oy
phân biệt không đối nhau.
- Trên Ox dựng đoạn OM = AB = 3cm
và dựng đoạn MN = CD = 5cm sao cho M nằm giữa O và N
- Trên tia Oy dựng đoạn OP = EF = 2cm.
- Dựng đường thẳng PM.
- Từ N dựng đường thẳng song song với PM cắt tia Oy tại Q.
Đoạn thẳng PQ = a cần dựng..
* Chứng minh:
Theo cách dựng, ta có: PM // NQ.
Trong ΔONQ ta có: PM // NQ

Ta có: CA=3,6cm =>CB=AB-CA=6-3,6=2,4cm
=> CA/CB=3,6/2,4=3/2
=> DA/DB=3/2
Mà ta có DA-DB=AB=6 cm ( Do điểm B nằm giữa A và D)
Áp dụng hiệu tỉ ta có:
DA=6:(3-2).3=18(cm)
2/\(\frac{AB}{CD}=\frac{2}{3}\Rightarrow\frac{AB}{2}=\frac{CD}{3}\Rightarrow\frac{AB}{4}=\frac{CD}{6}\)
\(\frac{CD}{EF}=\frac{4}{6}=\frac{2}{3}\Rightarrow\frac{CD}{2}=\frac{EF}{3}\Rightarrow\frac{CD}{6}=\frac{EF}{9}\)
=>\(\frac{AB}{4}=\frac{CD}{6}=\frac{EF}{9}=\frac{AB+CD+EF}{4+6+9}=\frac{70}{19}\)
=>AB=280/19 cm
CD=420/19 cm
EF=630/19 cm
Chúc e hc tốt :)
Cô giáo của mk kết quả lại ra AB=16cm ,CD=24cm ,EF=30cm. mk ko hiểu là sai ở đâu ạ

Để AB và CD tỉ lệ với PQ và EF thì \(\dfrac{6}{8}=\dfrac{4}{x}\)
=>\(x=4\cdot\dfrac{8}{6}=\dfrac{32}{6}=\dfrac{16}{3}\left(cm\right)\)

Bài 16:
Nếu giống ở bài thì phải là \(AB=3cm,CD=5cm\) nhé.
Cách dựng:
- Dựng hai tia chung gốc \(Ox\) và \(Oy\) phân biệt không đối nhau.
- Trên \(Ox\) dựng đoạn \(OM=AB=3cm\) và dựng đoạn \(MN=CD=5cm\) sao cho M nằm giữa O và N.
- Trên tia \(Oy\) dựng đoạn \(OP=EF=2cm.\)
- Dựng đường thẳng \(PM.\)
- Từ N dựng đường thẳng song song với \(PM\) cắt tia \(Oy\) tại Q. Ta được đoạn thẳng \(PQ=a\) cần dựng.
Chứng minh:
+ Xét \(\Delta ONQ\) có:
\(PM\) // \(NQ\) (do cách dựng).
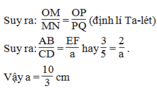
=> \(\frac{OM}{MN}=\frac{OP}{PQ}\) (định lí Ta - lét).
=> \(\frac{AB}{CD}=\frac{EF}{a}\)
=> \(\frac{3}{5}=\frac{2}{a}\)
=> \(a=2:\frac{3}{5}\)
=> \(a=\frac{10}{3}\left(cm\right).\)
Vậy \(a=\frac{10}{3}\left(cm\right).\)
Chúc bạn học tốt!